Corrélation entre l'activité solaire et les grands séismes dans le monde

Résumé

Les grands séismes qui se produisent dans le monde sont depuis longtemps reconnus comme n'ayant pas de distribution de Poisson, impliquant ainsi un mécanisme de corrélation à grande échelle, qui pourrait être interne ou externe à la Terre. Jusqu'à présent, aucune corrélation statistiquement significative de la sismicité globale avec l'un des mécanismes possibles n'a encore été démontrée. Dans cet article, nous analysons 20 ans de données sur la densité et la vitesse des protons, telles qu'enregistrées par le satellite SOHO, et la sismicité mondiale au cours de la période correspondante, telle que rapportée par le catalogue ISC-GEM. Nous avons trouvé une corrélation claire entre la densité de protons et l'occurrence de grands séismes ( M  > 5,6), avec un décalage temporel d'un jour.

La signification d'une telle corrélation est très élevée, avec une probabilité de se tromper inférieure à 10^–5. La corrélation augmente avec le seuil de magnitude du catalogue sismique. Un modèle provisoire expliquant une telle corrélation est également proposé, en termes d'effet piézoélectrique inverse induit par le champ électrique appliqué lié à la densité de protons. Ce résultat ouvre de nouvelles perspectives dans les interprétations sismologiques, ainsi que dans la prévision des séismes.

introduction

La sismicité mondiale ne suit pas une distribution de Poisson ¹ , même pas localement ² . De nombreux auteurs ont proposé des distributions statistiques spécifiques pour décrire un tel comportement non-poissonien ^{3 , 4 , 5 , 6 , 7} mais aucune d'entre elles n'est vraiment satisfaisante, probablement parce que le processus physique sous-jacent n'a pas été vraiment compris. De nombreux auteurs ont émis l'hypothèse qu'une composante de marée peut apparaître dans l'activité sismique (par exemple ^{8 , 9} ) mais des preuves généralisées n'ont jamais été prouvées. Tout récemment, certains auteurs ¹⁰ont suggéré que l'occurrence des tremblements de terre pourrait être liée aux variations de la vitesse de rotation de la Terre. Il y a aussi un plus petit nombre de chercheurs qui ont étudié les liens possibles entre l'activité solaire, les orages électromagnétiques et les tremblements de terre (par exemple ^{11 , 12 , 13 , 14 , 15 , 16} ). La première idée que les taches solaires pourraient influencer l'occurrence du tremblement de terre remonte à 1853, et est due au grand astronome solaire Wolf ¹⁷ . Depuis lors, un certain nombre de scientifiques ont rapporté une sorte de relation entre l'activité solaire et l'occurrence des tremblements de terre ^{16 , 18 , 19} ; ou parmi la sismicité globale et la variation géomagnétique ^{15, 20} ou orages magnétiques ^{21 , 22} . De plus, certains mécanismes ont été proposés pour justifier de telles corrélations : de petits changements induits par le couplage Soleil-Terre dans la vitesse de rotation de la Terre ²³ ; courants électriques de Foucault induits dans les défauts, les échauffant et diminuant la résistance au cisaillement ²⁴ ; ou augmentation piézoélectrique de la contrainte de défaut causée par les courants induits ²⁵ . Cependant, aucune de ces études n'a permis d'aboutir à une conclusion statistiquement significative sur la probabilité de tels mécanismes. Au contraire, ²⁶a fait valoir qu'il n'y a pas d'argument convaincant, statistiquement fondé, démontrant une interaction solaire-terrestre favorisant l'occurrence des tremblements de terre. Cependant, le grand intérêt de nos jours pour les interactions possibles entre l'occurrence des tremblements de terre et l'activité extraterrestre (principalement solaire), est attesté par exemple par le projet CSES-LIMADOU, une coopération sino-italienne visant à lancer un satellite pour étudier depuis l'espace l'influence possible de l'activité solaire et des modifications ionosphériques sur la sismicité ²⁷. Dans cet article, nous établirons définitivement l'existence d'une corrélation entre l'activité solaire et la sismicité globale, en utilisant un long ensemble de données et une analyse statistique rigoureuse. Une fois qu'une telle corrélation est démontrée, nous proposons un mécanisme provisoire, pour le moment qualitatif, d'une éventuelle interaction soleil-séisme.

Évaluation statistique de la corrélation activité solaire–séismes

Puisque notre objectif était de vérifier l'existence d'un lien entre l'activité solaire et les séismes, nous avons considéré deux ensembles de données : les séismes mondiaux et les mesures de protons du satellite SOHO.

En ce qui concerne les séismes, nous avons utilisé le catalogue ISC-GEM ²⁸ . Nous l'avons choisi car, à l'heure actuelle, il s'agit du seul ensemble de données mondiales avec des estimations de magnitude homogènes permettant une analyse statistique solide. Nous avons sélectionné ce catalogue car c'est le seul complet, avec des magnitudes homogènes, mais seulement à partir de M = 5,6. Il regroupe en effet l'ensemble des solutions Global CMT ^{29 , 30} et ajoute environ 10 % des événements manqués par ces dernières. Dans ce cas, les grandeurs sont exprimées sous forme de proxys mb et Ms. Nous avons vérifié son exhaustivité pour M  5,6 depuis 1996. Le catalogue des séismes actuellement ( ver.7.0) va jusqu'à la fin de 2016. Les catalogues de séismes que nous avons utilisés tout au long de cet article, avec un seuil de magnitude progressivement plus grand, sont rapportés dans le tableau 1 .

Tableau 1 Ensembles de données sur les tremblements de terre utilisés dans ce document.

Tableau pleine grandeur

Le satellite SOHO (Solar and Heliospheric Observatory) est situé au point L 1 de Lagrange à environ 1,5 millions de kilomètres de la Terre. Les données horaires en termes de densité de protons ρ et de vitesse v sont disponibles pour environ 85 % du temps depuis le début de 1996. En combinant les deux variables du catalogue, nous pourrions déduire, comme variables supplémentaires, le flux de protons ρv , et la pression dynamique ρv ² /2. Nous avons donc considéré, dans nos analyses, quatre variables protoniques différentes V : le flux, la pression dynamique, la vitesse et la densité. Nous avons calculé la moyenne de chaque variable protonique dans des intervalles quotidiens consécutifs. Dans le tableau 2nous rapportons les valeurs minimales, maximales et moyennes pour chaque variable V .

Tableau 2 Les quatre variables V que nous avons utilisées dans cet article.

Tableau pleine grandeur

Dans un premier temps, chacune de ces variables V a été comparée aux événements sismiques mondiaux avec M  5,6 dans la période 1996/01/21-2016/12/31, en considérant le nombre quotidien d'événements uniquement. Le choix de cet ensemble de données est dû au fait qu'il est le plus grand. Le nombre journalier d'événements est plus important que le moment total journalier, puisque nous nous intéressons au nombre de processus de rupture individuels, plutôt qu'à une quantité qui s'étend sur plusieurs ordres de grandeur. De plus, pour un grand nombre d'événements, sur quelques milliers, la relation de Gutenberg Richter ³¹est universellement valable et, puisque les tremblements de terre sont autosimilaires, le nombre d'événements reflète de manière équivalente la taille du choc principal. Nous avons également choisi de ne pas dégrouper l'ensemble de données d'événements pour deux raisons. Premièrement, selon ³² , il est erroné de faire la distinction entre les événements principaux, les répliques et l'activité de fond ; deuxièmement, le dégroupage est quelque peu arbitraire mais aboutirait de toute façon à un catalogue complètement non corrélé, détruisant probablement les informations clés que nous recherchons.

La densité et la vitesse des protons varient avec le temps, donc s'il existe une corrélation avec les séismes, elle doit être trouvée soit en termes de taux de séismes différents en fonction des valeurs de protons élevées/faibles, soit avant/après les valeurs élevées ou faibles. Nous avons donc décidé d' étudier 5 conditions qui sont illustrées dans le tableau 3 .

Tableau 3 Les 5 conditions examinées pour vérifier une éventuelle corrélation avec les séismes, étant donné un seuil V _T pour l'une des variables V .

Tableau pleine grandeur

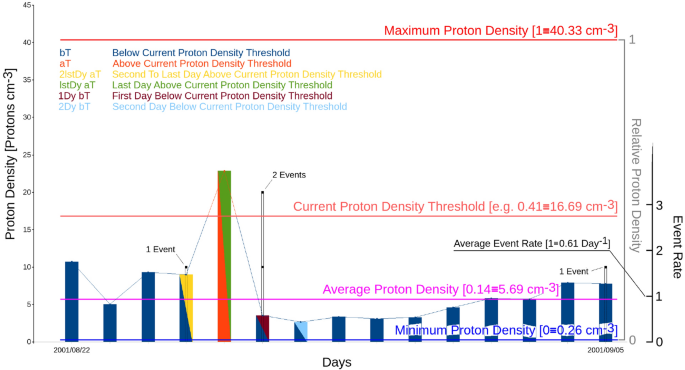
La figure  1 montre, avec un exemple réalisé sur 15 jours de catalogue, la procédure globale et illustre le sens des conditions utilisées pour les tests statistiques.

Figure 1

 

La figure montre un exemple d'application de la méthode statistique à 15 jours du catalogue. Les niveaux d'histogramme donnent la valeur quotidienne de la densité de protons ; la ligne rouge indique le niveau du seuil de densité de courant (toutes les valeurs de celui-ci sont testées consécutivement). Les points noirs indiquent la survenue de tremblements de terre ce jour-là. Les couleurs de l'histogramme indiquent les conditions qui sont appliquées pour les tests statistiques ; en particulier, le violet indique le premier jour en dessous du seuil de densité de protons actuel (c'est-à-dire le premier jour après une valeur au-dessus du seuil), le vert indique le dernier jour au-dessus du seuil de densité, et ainsi de suite (comme indiqué dans la légende). Des valeurs élevées de fréquence des tremblements de terre dans l'une de ces périodes particulières indiquent la tendance des tremblements de terre à se produire avant, pendant,après (et avec quel décalage) une période de densité protonique supérieure au seuil de courant. La figure montre également les valeurs minimale (bleu), moyenne (violet) et maximale (rouge intense) de la densité de protons pour l'ensemble du catalogue utilisé.

Image en taille réelle

Une autre remarque importante est que puisque nous considérons 4 variables, 5 conditions et, plus loin dans la discussion, 6 seuils de magnitude avec différentes fenêtres temporelles, nous choisissons d'utiliser des algorithmes non dimensionnels, pour faciliter la comparaison.

La première étape consiste à calculer la moyenne de V ( V _av ) . En raison de la nécessité de travailler avec des variables non dimensionnelles, nous exprimons la moyenne non dimensionnelle de V ( V _{av_ad} ) comme

Vav−ad=(Vav−Vmin)/(Vmax−Vmin)

(1)

approximé au deuxième chiffre significatif. Ensuite, nous définissons un seuil variable, comme

VT=Vmin+Vstep(Vmax−Vmin)

(2)

pour chaque variable V , où V _step va de la valeur moyenne de V _{av_ad} à 1, avec des pas de 0,01. Pour une condition C donnée, et pour chaque V _T , on peut compter le nombre D _C de jours qui satisfont la condition et le nombre correspondant d'événements E _C se produisant dans ces jours. D et E sont respectivement le nombre de jours où les données SOHO sont disponibles et le nombre total d'événements qui se produisent ces jours-là. De cette façon pour chaque V _T , nous pouvons simplement définir un taux relatif d'événement

R = (EC/réC) / [ ( E−EC) / ( D −réC) ]

(3)

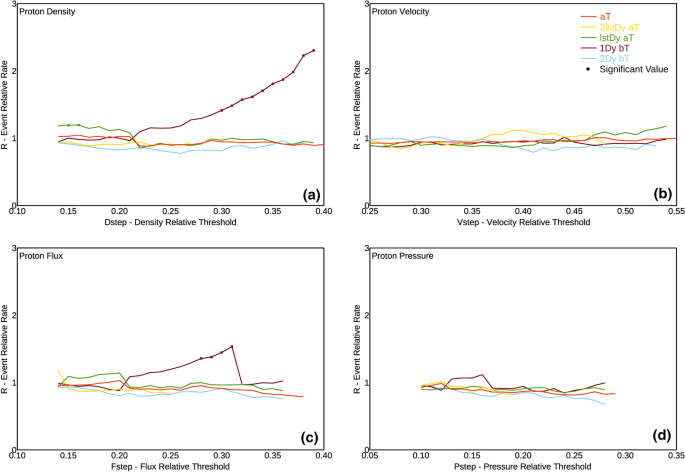
Sur la figure  2, nous montrons le taux relatif d'événement R par rapport à V _step , pour chaque condition C, représenté pour les 4 variables : flux, pression dynamique, vitesse et densité. Cette approche implique que, si des tremblements de terre se produisent accidentellement par rapport aux variables protoniques V , le taux relatif de l'événement R devrait osciller autour de 1, dans une incertitude aléatoire.

Figure 2

 

Tracés du taux relatif d'événement (voir l'équation  2 ) en fonction du seuil de densité non dimensionnel, pour : ( a ) le flux de protons ; ( b ) pression dynamique du proton; ( c ) vitesse du proton; ( d ) densité de protons. Différentes couleurs font référence à différentes conditions, comme expliqué dans le tableau 2 . Les carrés font référence à des valeurs qui présentent une corrélation statistiquement significative à un niveau de signification de 0,00001.

Image en taille réelle

Pour la plupart des CV paires représentées sur la figure.  2 , nous avons arrêté le calcul à V _étape ≈  0,4. Ceci est dû au fait que, pour des valeurs de seuil plus élevées, D _C / D devient inférieur à 0,015, donnant ainsi un échantillonnage trop mauvais. Cette valeur a été sélectionnée pour avoir au moins environ 100 jours satisfaisant la condition sélectionnée.

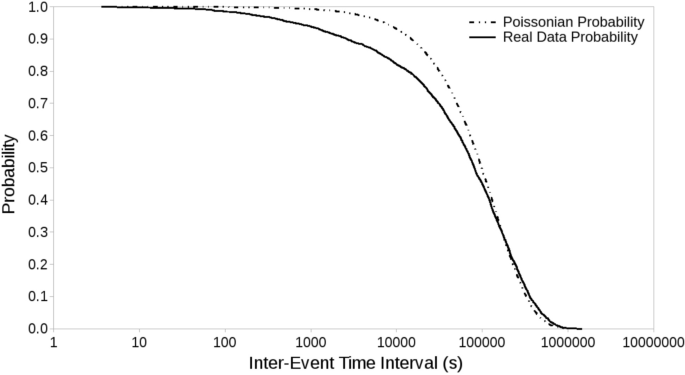
La dernière étape consiste à évaluer si R est significativement différent de 1, pour l'une quelconque des variables V, dans l'une quelconque des conditions C à l' intérieur d'une plage V _T. Cela signifie que nous devons concevoir un test en partant de l'hypothèse que l'occurrence des tremblements de terre n'est pas poissonienne ^{1 , 2 , 3 , 4 , 5 , 6 , 7} . Nous choisissons de créer 10 ⁵ensembles de données synthétiques, en utilisant les intervalles de temps entre les événements de données réelles combinés de manière aléatoire. Cette approche empirique nous assure un catalogue synthétique qui a exactement les mêmes propriétés statistiques que le catalogue réel, puisque nous obtenons un ensemble de données aléatoires avec la même fonction de survie que le vrai. La fonction de survie donne la probabilité d'occurrence des intervalles de temps entre les événements et est couramment utilisée pour décrire les propriétés statistiques de l'occurrence des tremblements de terre (par exemple ^{1 , 4} ). Nous avons suivi cette approche empirique car, comme indiqué ci-dessus, il n'y a pas de distribution satisfaisante qui décrit les intervalles de temps entre les événements dans une série d'événements non dégroupée. Pour clarifier notre approche, dans la Fig. 3 nous comparons la fonction de survie à un événement réel avec une fonction poissonienne avec un taux d'événement identique. Comme il est clair, les temps d'inter-arrivée du catalogue réel sont nettement différents d'une distribution de Poisson.

figure 3

 

Distribution temporelle inter-arrivée des événements dans le catalogue sismique (trait plein). La ligne pointillée montre, à titre de comparaison, la distribution attendue des temps inter-arrivées pour une distribution de Poisson avec le même taux d'événements.

Image en taille réelle

Nous voulions donc tester chaque fois qu'une distribution aléatoire pouvait produire les mêmes effets, en termes de valeurs R , que la vraie. Ce n'est que si, pour un V _T donné , R est supérieur à l'une des valeurs R _rand obtenues par des distributions d'intervalles de temps distribuées aléatoirement, nous considérons cette valeur comme significative, indiquant ainsi clairement une corrélation. Cette technique de bootstrap correspond à effectuer un test statistique avec l'hypothèse nulle que la corrélation observée n'est que fortuite ; étant donné le nombre de 10 ⁵ réalisations considérées, on peut rejeter l'hypothèse nulle, pour les cas significatifs dans lesquels aucune valeur de Rest supérieur ou égal à celui observé, avec une probabilité de se tromper inférieure à 0,00001. Sur la figure  2, nous montrons les valeurs statistiquement significatives de R , telles qu'elles étaient précédemment définies, sous forme de carrés. Nous tenons à souligner que ce critère est extrêmement rigoureux (le niveau de confiance est très élevé, 99,999 %, par rapport aux niveaux normalement utilisés de 95 à 99 %), mais en fait notre objectif est de démontrer, hors de tout doute raisonnable, si la corrélation entre toutes les variables protoniques et les tremblements de terre existent. Pour la même raison, nous avons utilisé toutes les données protons disponibles, même lorsqu'un seul jour était précédé et suivi de données manquantes : cela a évidemment conduit à une sous-estimation de la valeur R , et donc de la significativité.

Les analyses décrites jusqu'à présent, représentées sur la figure  2 , montrent que la condition 1Dy bT dans le tableau 2 (c'est-à-dire un jour après la diminution de la variable en dessous de la valeur seuil) est la seule significative, et uniquement pour ρ (densité) et ρν ( flux) variables. De plus elle augmente de façon monotone au fur et à mesure que la valeur de seuil augmente, au moins jusqu'à des valeurs de seuil pas trop élevées, où l'échantillonnage devient trop pauvre. Une telle tendance à la hausse de la valeur de crête R est mieux observée pour la densité ρ , mais elle peut également être observée, bien qu'avec des valeurs de crête plus faibles, pour le flux ρv. Nous pouvons donc affirmer que la corrélation la plus frappante entre les variables protoniques et la sismicité globale est avec les séismes se produisant au cours du 1er jour après que la valeur de densité ρ diminue en dessous d'un certain seuil, dans la plage de _pas V de 0,31 à 0,39. Une telle plage pour le _pas V correspond à une plage de densité de protons comprise entre 12,7 et 15,9 coups cm ^-2 .

Dans une dernière étape, nous avons en outre vérifié la dépendance des valeurs de pic R observées sur le seuil de magnitude du catalogue des séismes. Nous avons ensuite progressivement augmenté le seuil de magnitude inférieure du catalogue sismique utilisé selon le tableau 1 .

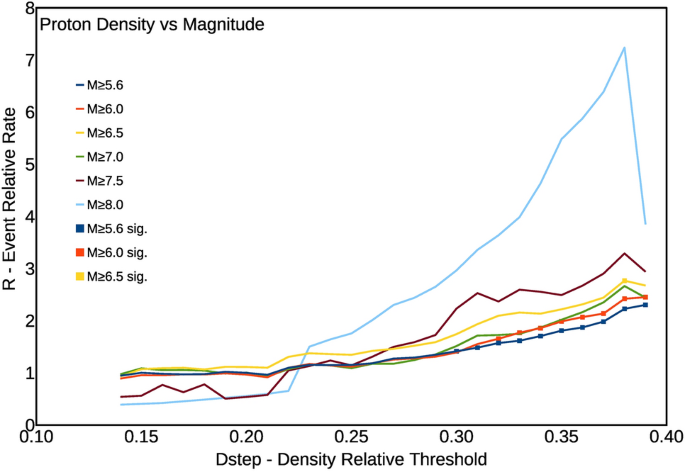
La figure  4 montre clairement le pic de corrélation qui devient de plus en plus grand avec l'augmentation de la coupure d'amplitude. Ces résultats confirment l'existence d'une corrélation fortement significative entre les séismes mondiaux et la densité de protons au voisinage de la magnétosphère, due à l'activité solaire.

Figure 4

 

Tracés du taux relatif de l'événement R en fonction de la densité de protons normalisée, et pour la condition 1Dy bT (séismes se produisant dans les 24 h à partir de la valeur de la densité décroissant en dessous de la valeur seuil). Les couleurs indiquent différentes amplitudes de coupure inférieures dans le catalogue.

Image en taille réelle

Test et discussion des résultats statistiques

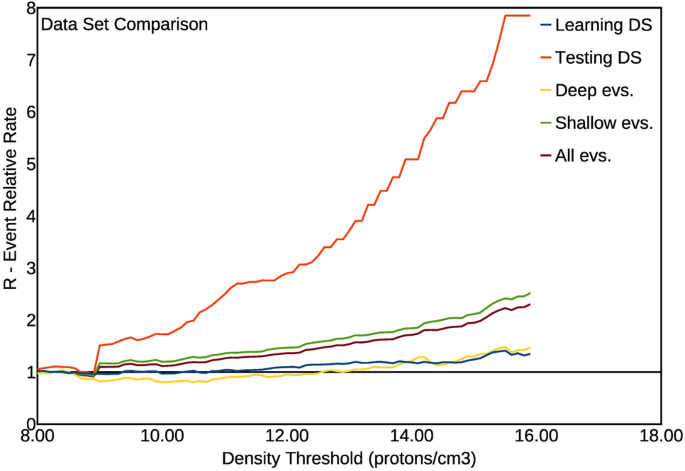
Une autre façon de vérifier la robustesse de la corrélation inférée consiste à diviser le catalogue en deux parties, en utilisant la première moitié (1996-2005) pour déduire les meilleurs paramètres de corrélation, puis en appliquant les paramètres inférés à la seconde moitié (2006-2016). ) pour voir s'il continue d'indiquer une corrélation significative. Il s'agit d'un test classique pour vérifier que la corrélation inférée n'est pas simplement le résultat d'un surajustement des données. La première partie du catalogue est l'ensemble « d'apprentissage », tandis que la seconde partie est l'ensemble « d'essai ». Si les résultats obtenus avec l'ensemble de test, en utilisant les critères optimaux déduits de celui d'apprentissage, indiquent également une corrélation significative, alors une telle corrélation est robuste et pas seulement un surajustement des données. Nous avons ensuite divisé le catalogue en deux parties, chacune d'une durée de 10 ans comme indiqué précédemment,et déduit le meilleur modèle de la première partie. Nous avons en fait déduit, en tant que meilleur modèle (de score R le plus élevé) de la première moitié du catalogue, le lendemain du jour où le pic de densité de protons diminue en dessous du seuil ; puis, nous avons calculé le score R obtenu, avec le même modèle, à partir de la seconde moitié du catalogue. Nous avons ensuite généralisé ce test, afin de vérifier également les performances relatives des différents catalogues contenant respectivement les séismes peu profonds (Profondeur < 60 km) et profonds (Profondeur > 60 km). Cette subdivision supplémentaire est également intéressante, pour deux raisons : premièrement, le mécanisme des événements profonds pourrait être en principe quelque peu différent de ceux de la croûte ; deuxièmement (et quelque peu liés), car ils ne sont généralement pas suivis de séquences de répliques soutenues.Le catalogue des événements profonds est alors un catalogue naturellement « dégroupé », et il peut donc aider à comprendre comment la corrélation densité de protons-séisme fonctionnerait pour un catalogue dégroupé. Évidemment, le processus de déclusterisation artificielle est hautement subjectif, et pourrait alors détruire les principales caractéristiques du catalogue liées à la corrélation³³ . Les résultats obtenus pour le score R avec ces différentes subdivisions du catalogue sont présentés sur la figure  5 , et comparés aux résultats obtenus avec l'ensemble du catalogue (déjà montré sur la figure  2 a). Comme on le voit, toutes les courbes, pour tous les sous-catalogues, montrent une nette augmentation du score R en fonction du seuil de densité protonique utilisé. Cela montre clairement que l'effet de l'augmentation de la sismicité avec l'augmentation de la densité de protons se produit toujours. Le niveau de signification pour accepter la corrélation observée, calculé de la même manière expliquée pour la figure  2(c'est-à-dire générer aléatoirement de nombreux catalogues partageant la même distribution d'événements que la vraie) va de 0,001 du catalogue d'apprentissage et du catalogue des événements profonds à 0,00001 du catalogue complet, du catalogue des événements superficiels et du catalogue de test. On devrait donc conclure, de ce test, que la corrélation observée est toujours significative, qu'elle ne représente pas un surajustement des données (car les mêmes paramètres inférés du catalogue d'apprentissage décrivent aussi bien celui du test), et que le catalogue des seuls les événements profonds montrent une corrélation avec la densité de protons. Notons aussi, cependant, que l'activité solaire (densité protonique) dans la deuxième partie du catalogue est nettement plus faible que dans la première partie ; et une telle diminution est particulièrement marquée dans la dernière période (2013-2016) où,pour un seuil de densité donné, il y a moins de pics de densité et par conséquent moins de périodes de 24 h suivant les pics de densité.

Figure 5

 

Tracés du taux relatif de l'événement R en fonction de la valeur absolue de la densité de protons, et pour la condition 1Dy bT (séismes se produisant dans les 24 h à partir de la valeur de la densité décroissant en dessous de la valeur seuil). Les couleurs indiquent les différentes subdivisions du catalogue (les résultats pour le catalogue total sont représentés par la courbe marron).

Image en taille réelle

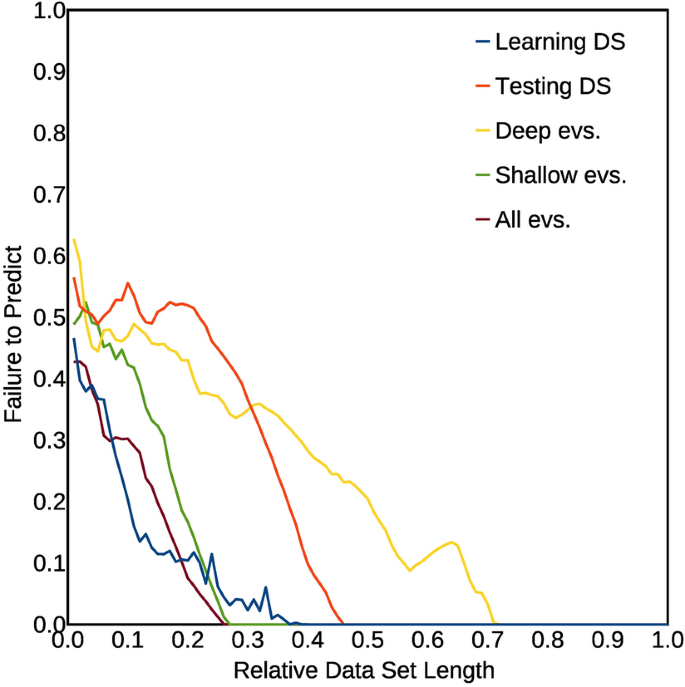
Il peut être encore plus intéressant de voir ce qui se passe en subdivisant le catalogue en parties plus petites, et d'étudier la qualité du modèle inféré obtenu pour différentes subdivisions, progressivement plus grandes, du catalogue. La procédure utilisée ici comme test pour la corrélation inférée a été adaptée du concept du diagramme de Molchan ³⁴. Nous avons commencé à considérer une fenêtre temporelle dont la longueur en jours est de 0,01 du catalogue total : 0,01 × 6 774 = 67,74, arrondi à 68 jours. On considère alors toutes les parties d'une durée de 68 jours dans le catalogue, en faisant glisser progressivement les fenêtres de 68 jours de 1 jour à chaque étape, jusqu'à ce que le 68ème jour corresponde au jour de fin du catalogue. De cette façon, nous obtenons 6 774 − 68 = 6 706 fenêtres temporelles. Pour chaque fenêtre temporelle, nous calculons si le taux relatif d'événements R, pour les événements survenant dans les 24 h suivant la fin d'un pic de densité, est supérieur ou inférieur au nombre moyen d'événements par jour calculé à partir de l'ensemble du catalogue (0,95 événements/jour ) : s'il est supérieur, le résultat de la prédiction est positif, sinon il est négatif. Dans le cas où il n'y a, dans une fenêtre temporelle donnée, aucun jour survenant après la fin d'un pic de densité, cette fenêtre est exclue du décompte. Sur l'axe Y,nous avons indiqué la fraction des fenêtres temporelles glissantes avec un échec de prédiction. Ensuite, nous répétons la même procédure et le même calcul pour des fenêtres temporelles de plus en plus grandes, d'une fraction de 0,01 à 1 de la durée totale du catalogue ; pour chaque longueur fractionnaire de la fenêtre glissante, indiquée sur l'axe X, nous reportons sur l'axe Y la fraction d'échecs de prédiction. Il est évident que, pour un résultat totalement aléatoire, la fraction d'échecs de prédiction est d'environ 0,5 ; un nombre significativement plus petit indique une corrélation significative, alors qu'un nombre significativement plus élevé indiquerait une anti-corrélation significative. Nous avons appliqué cette procédure à tous les sous-catalogues considérés ici (catalogue d'apprentissage, catalogue de test, catalogue d'événements superficiels, catalogue d'événements profonds) ainsi qu'à l'ensemble du catalogue. ChiffreChiffreChiffreChiffreChiffreon répète la même procédure et le même calcul pour des fenêtres temporelles de plus en plus grandes, d'une fraction de 0,01 à 1 de la durée totale du catalogue ; pour chaque longueur fractionnaire de la fenêtre glissante, indiquée sur l'axe X, nous reportons sur l'axe Y la fraction d'échecs de prédiction. Il est évident que, pour un résultat totalement aléatoire, la fraction d'échecs de prédiction est d'environ 0,5 ; un nombre significativement plus petit indique une corrélation significative, alors qu'un nombre significativement plus élevé indiquerait une anti-corrélation significative. Nous avons appliqué cette procédure à tous les sous-catalogues considérés ici (catalogue d'apprentissage, catalogue de test, catalogue d'événements superficiels, catalogue d'événements profonds) ainsi qu'à l'ensemble du catalogue. Chiffreon répète la même procédure et le même calcul pour des fenêtres temporelles de plus en plus grandes, d'une fraction de 0,01 à 1 de la durée totale du catalogue ; pour chaque longueur fractionnaire de la fenêtre glissante, indiquée sur l'axe X, nous reportons sur l'axe Y la fraction d'échecs de prédiction. Il est évident que, pour un résultat totalement aléatoire, la fraction d'échecs de prédiction est d'environ 0,5 ; un nombre significativement plus petit indique une corrélation significative, alors qu'un nombre significativement plus élevé indiquerait une anti-corrélation significative. Nous avons appliqué cette procédure à tous les sous-catalogues considérés ici (catalogue d'apprentissage, catalogue de test, catalogue d'événements superficiels, catalogue d'événements profonds) ainsi qu'à l'ensemble du catalogue. Chiffrepour chaque longueur fractionnaire de la fenêtre glissante, indiquée sur l'axe X, nous reportons sur l'axe Y la fraction d'échecs de prédiction. Il est évident que, pour un résultat totalement aléatoire, la fraction d'échecs de prédiction est d'environ 0,5 ; un nombre significativement plus petit indique une corrélation significative, alors qu'un nombre significativement plus élevé indiquerait une anti-corrélation significative. Nous avons appliqué cette procédure à tous les sous-catalogues considérés ici (catalogue d'apprentissage, catalogue de test, catalogue d'événements superficiels, catalogue d'événements profonds) ainsi qu'à l'ensemble du catalogue. Chiffrepour chaque longueur fractionnaire de la fenêtre glissante, indiquée sur l'axe X, nous reportons sur l'axe Y la fraction d'échecs de prédiction. Il est évident que, pour un résultat totalement aléatoire, la fraction d'échecs de prédiction est d'environ 0,5 ; un nombre significativement plus petit indique une corrélation significative, alors qu'un nombre significativement plus élevé indiquerait une anti-corrélation significative. Nous avons appliqué cette procédure à tous les sous-catalogues considérés ici (catalogue d'apprentissage, catalogue de test, catalogue d'événements superficiels, catalogue d'événements profonds) ainsi qu'à l'ensemble du catalogue. Chiffreun nombre significativement plus petit indique une corrélation significative, alors qu'un nombre significativement plus élevé indiquerait une anti-corrélation significative. Nous avons appliqué cette procédure à tous les sous-catalogues considérés ici (catalogue d'apprentissage, catalogue de test, catalogue d'événements superficiels, catalogue d'événements profonds) ainsi qu'à l'ensemble du catalogue. Chiffreun nombre significativement plus petit indique une corrélation significative, alors qu'un nombre significativement plus élevé indiquerait une anti-corrélation significative. Nous avons appliqué cette procédure à tous les sous-catalogues considérés ici (catalogue d'apprentissage, catalogue de test, catalogue d'événements superficiels, catalogue d'événements profonds) ainsi qu'à l'ensemble du catalogue. Chiffre 6 montre les résultats d'une telle analyse, pour le seuil de densité le mieux adapté, calculé pour le catalogue total, de 15,5 protons/cm ³ . Les résultats synthétisés dans la Fig.6 sont efficaces pour donner une image complète et claire de la robustesse des résultats, puis de la corrélation inférée. En effet, ils montrent clairement des valeurs de fraction d'échec, pour le catalogue d'apprentissage, le catalogue de test et le catalogue total, qui sont nettement inférieures à 0,5, sauf pour des fenêtres temporelles très faibles. L'intégrale sous les courbes respectives représente ici la fraction de rupture totale : elle varie d'un minimum de 0,05 pour le catalogue d'apprentissage et l'ensemble du catalogue, à un maximum de 0,21 pour le catalogue des séismes profonds. Il est également intéressant de noter que certains catalogues montrent des résultats encore meilleurs avec des seuils de densité légèrement différents. Le catalogue des séismes profonds, par exemple, présente une fraction de défaillance totale de seulement 0,14 pour un seuil de densité légèrement supérieur : 16,1 protons/cm ³; le catalogue « test » a un meilleur minimum de fraction de défaillance totale de 0,14 pour un seuil de densité inférieur : 13,3 protons/cm ³ . Ainsi, toutes les valeurs obtenues de la fraction de défaillance globale sont considérablement inférieures à 0,5, confirmant ainsi la prédictivité de la méthode, puis la significativité de la corrélation. Notons que la méthode que nous utilisons ici diffère conceptuellement du diagramme de Molchan également pour la forme de l'espace mis en jeu pour discriminer des résultats purement aléatoires d'une corrélation significative. En fait, un résultat purement aléatoire est représenté comme la diagonale d'un carré de surface normalisée à 1,0 dans le diagramme de Molchan ³⁴; dans notre méthode, à l'inverse, un résultat purement aléatoire est représenté par une ligne horizontale de valeur constante Y = 0,5. Dans les deux diagrammes, la surface (intégrale) sous une courbe représentant des résultats purement aléatoires a une valeur d'environ 0,5 ; des valeurs significativement plus faibles indiquent, au contraire, un degré significatif de prédictivité.

Figure 6

 

Diagrammes montrant la fraction d'échec à prévoir en fonction de la longueur des fenêtres temporelles glissantes dans lesquelles le catalogue est subdivisé. La longueur est indiquée, sur l'axe X, normalisée à la longueur totale du catalogue. Les courbes des différents catalogues sont représentées avec des couleurs différentes (voir aussi le texte). Les résultats présentés ici ont été calculés en utilisant la valeur du seuil de densité de protons ρ _T  = 15,5 protons/cm ³, qui représente la valeur optimale, qui minimise l'intégrale sous la courbe pour le catalogue total. La valeur de l'intégrale sous chaque courbe représente la fraction de défaillance totale de la prédiction ; il doit être proche de 0,5 pour un modèle aléatoire non prédictif. Les valeurs trouvées ici sont : 0,05 pour le catalogue total ; 0,05 pour le catalogue « apprentissage » ; 0,08 pour le catalogue des événements peu profonds ; 0,17 pour le catalogue 'tests' ; 0,21 pour le catalogue des événements profonds.

Image en taille réelle

Tous les résultats et tests obtenus soulignent que la corrélation entre les séismes et la densité de protons est hautement statistiquement significative, même si pour les catalogues avec des seuils de magnitude de séisme trop élevés, elle ne passe pas strictement le test de signification. Cela est dû au fait que les trois ensembles de données de magnitude plus élevée ( M  7,0, 7,5, 8,0) sont composés d'un très petit nombre d'événements (tableau 1 ) et de plus, pour cette raison, la relation de Gutenberg-Richter n'est plus valide.

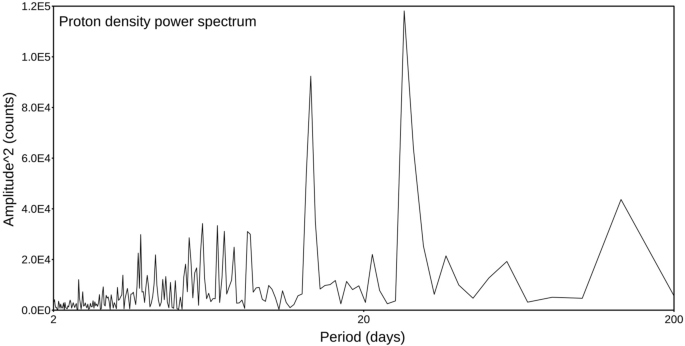
Comme test final, nous avons voulu vérifier si le catalogue de densité de protons est complètement décorrélé. Nous savons, comme indiqué ci-dessus, que le catalogue sismique des forts séismes est non-poissonien et corrélé en interne, nous avons donc analysé la série de densité de protons pour vérifier si elle était caractérisée par un spectre de bruit blanc qui indiquerait un processus non corrélé. Nous avons simplement calculé le spectre de puissance, qui est montré dans la Fig.  7; il est clairement très différent d'un spectre blanc, présentant au moins deux pics nets. Nous avons effectué un tel calcul sur la plus longue fenêtre de temps ininterrompue qui a une durée de 405 jours. Cette preuve atteste que ni la distribution de la densité de protons n'est aléatoire. Ainsi, cela confirme définitivement que la corrélation observée entre le catalogue sismique et la densité de protons ne peut vraisemblablement pas être obtenue par hasard ; parce que la probabilité que deux quantités, chacune d'entre elles corrélées de manière interne, montrent une corrélation mutuelle claire seulement par hasard est négligeable.

Figure 7

 

Spectre de puissance calculé pour le catalogue de densité de protons. Le spectre est calculé uniquement pour la période consécutive maximale de données sans interruption, d'une durée de 200 jours.

Image en taille réelle

En conclusion, l'analyse du catalogue mondial des séismes 1996-2016 montre une corrélation significative avec la densité de protons mesurée sur la même période. Une telle corrélation est décrite par une plus grande probabilité que des tremblements de terre se produisent pendant des fenêtres temporelles de 24 h juste après une période de pointe (c'est-à-dire une période passée au-dessus d'un certain seuil) de densité de protons due à l'activité solaire. Ce type de corrélation entre la sismicité mondiale et l'activité solaire a également été vérifiée avec d'autres variables liées à l'activité solaire, notamment la vitesse des protons, la pression dynamique des protons, le flux de protons et la densité de protons. Cependant, une corrélation significative ne peut être observée qu'avec le flux de protons, en plus de la densité de protons. La corrélation est de toute façon beaucoup plus nette en utilisant une simple densité de protons,démontrant ainsi qu'il s'agit de la variable réellement influente pour déterminer la corrélation avec l'occurrence des tremblements de terre. Cette corrélation s'avère statistiquement très significative. La haute significativité de la corrélation observée est également renforcée par l'observation qu'en augmentant la magnitude seuil du catalogue des séismes, le pic de corrélation devient progressivement plus grand. L'application d'une autre méthodologie de test appropriée, utilisant des concepts similaires au diagramme de MolchanL'application d'une autre méthodologie de test appropriée, utilisant des concepts similaires au diagramme de MolchanL'application d'une autre méthodologie de test appropriée, utilisant des concepts similaires au diagramme de Molchan^{34 , 35} , confirme également la signification statistique de la corrélation observée. La corrélation entre les grands séismes mondiaux et la densité de protons modulée par l'activité solaire apparaît alors fortement évidente et significative.

Un possible modèle qualitatif pour expliquer les observations

Une fois qu'une forte corrélation entre la densité de protons, générée par le vent solaire, et les grands séismes mondiaux a été évaluée, la prochaine étape consiste à vérifier s'il existe un mécanisme physique qui pourrait expliquer un tel résultat. Plusieurs mécanismes ont été proposés, jusqu'à présent, pour le déclenchement solaire-terrestre des séismes (voir ²⁶ pour une revue). Bien que les observations antérieures sur le déclenchement solaire-terrestre n'aient pas été convaincantes ²⁶ , certains des mécanismes précédemment proposés pourraient expliquer nos résultats, qui sont au contraire statistiquement significatifs. En particulier, Sobolev et Demin ²⁵ont étudié les effets piézoélectriques dans les roches générés par de grands courants électriques. Notre corrélation observée implique qu'un potentiel électrique élevé se produit parfois entre l'ionosphère, chargée par la forte densité de protons générés à des distances plus élevées, et la Terre. Un tel potentiel élevé pourrait générer, à la fois de manière directe ou déterminante, par induction électrique, des altérations du potentiel souterrain normal, une décharge électrique, canalisée en profondeur par de larges failles, qui représentent des canaux préférentiels hautement conducteurs. Un tel courant électrique, traversant le défaut, générerait, par effet piézoélectrique inverse, une impulsion de contrainte/déformation qui, ajoutée à la charge du défaut et modifiant la contrainte coulombienne totale, pourrait déstabiliser le défaut favorisant sa rupture. L'effet piézoélectrique inverse serait dû, dans les roches,par les minéraux de quartz qui y sont abondants. Un tel effet peut fonctionner, en principe, pour toutes sortes de défauts. L'effet piézoélectrique, en effet, agit pour produire une impulsion de dilatation ou de contraction sur un axe particulier du cristal, en fonction de la polarité du courant électrique. Pour les cristaux de quartz distribués de manière aléatoire sur une surface de faille de n'importe quelle orientation, l'effet net est une impulsion de déformation/contrainte normale à la faille, car les autres composantes de déformation/contrainte se compensent entre elles dans les roches en vrac. La contrainte normale peut stabiliser ou déstabiliser tout type de défaut, selon le signePour les cristaux de quartz distribués de manière aléatoire sur une surface de faille de n'importe quelle orientation, l'effet net est une impulsion de déformation/contrainte normale à la faille, car les autres composantes de déformation/contrainte se compensent entre elles dans les roches en vrac. La contrainte normale peut stabiliser ou déstabiliser tout type de défaut, selon le signePour les cristaux de quartz distribués de manière aléatoire sur une surface de faille de n'importe quelle orientation, l'effet net est une impulsion de déformation/contrainte normale à la faille, car les autres composantes de déformation/contrainte se compensent entre elles dans les roches en vrac. La contrainte normale peut stabiliser ou déstabiliser tout type de défaut, selon le signe^{36 , 37 , 38} ; cependant, étant donné qu'il s'agit d'une impulsion transitoire, elle n'a d'effet que dans le cas où elle est capable d'augmenter instantanément la contrainte coulombienne totale sur une faille donnée au-dessus de la résistance à la rupture, générant ainsi le séisme ³⁶. Il ne représenterait alors qu'un petit effet déstabilisant sur une faille déjà chargée de manière critique. Ainsi, le cycle sismique serait de toute façon dominé par des phénomènes tectoniques, mais ce petit effet déclencheur externe pourrait générer la légère corrélation observée parmi les séismes mondiaux. Ces types d'effets, induits par un potentiel électrique élevé entre l'ionosphère et la Terre, devraient vraisemblablement s'accompagner de décharges électriques dans l'atmosphère, qui provoqueraient des phénomènes de luminescence. En fait, il existe de nombreuses observations de phénomènes de luminescence macroscopique (appelés Earthquake Lights) avant et accompagnant les grands séismes ³⁹. De plus, ces phénomènes pourraient également provoquer de forts effets électromagnétiques, qui seraient enregistrés sous forme d'ondes radio ; même de tels phénomènes ont été largement rapportés comme accompagnant et généralement précédant les grands séismes ⁴⁰ . Plus généralement, de nombreuses anomalies électromagnétiques, souvent bien évidentes, sont de plus en plus fréquemment rapportées associées à des séismes modérés à importants ⁴¹ . La littérature scientifique récente regorge d'hypothèses sur la manière dont de tels effets électromagnétiques, associés aux grands séismes, pourraient être générés. La question la plus débattue est de savoir s'ils peuvent être considérés comme des précurseurs (ou peut-être des déclencheurs) pour de grands événements, ou s'ils sont causés par le processus de glissement sur les failles qui génèrent également le séisme ^{42 , 43}. Nous suggérons ici que l'augmentation de la densité de protons près de la magnétosphère peut expliquer qualitativement toutes ces observations, et aussi donner une base physique à nos observations statistiques.

Conclusion

Cet article donne la première preuve, fortement statistiquement significative, d'une forte corrélation entre les grands séismes mondiaux et la densité de protons près de la magnétosphère, due au vent solaire. Ce résultat est extrêmement important pour la recherche sismologique et pour d'éventuelles implications futures sur la prévision des tremblements de terre. En effet, bien que le caractère non-poissonien, et donc la corrélation entre les séismes mondiaux à grande échelle, soit connu depuis plusieurs décennies, cela pourrait en principe s'expliquer par plusieurs mécanismes. Dans cet article, nous démontrons que cela peut probablement être dû à l'effet du vent solaire, modulant la densité de protons et donc le potentiel électrique entre l'ionosphère et la Terre. Bien qu'une analyse quantitative d'un modèle particulier et spécifique pour nos observations dépasse le cadre de cet article,nous pensons qu'un mécanisme physique possible et probable expliquant nos observations statistiques est l'impulsion de contrainte/déformation causée par des effets piézoélectriques inverses. De telles impulsions seraient générées par de grandes décharges électriques canalisées dans les grandes failles, en raison de leur conductivité élevée en raison de la jauge de faille fracturée et saturée d'eau. Les observations généralisées de plusieurs effets électromagnétiques macroscopiques avant, ou associés à de grands séismes, soutiennent notre modèle qualitatif pour expliquer la corrélation observée, hautement statistiquement significative, densité de protons-séismes. Il est important de noter que notre hypothèse implique seulement que la densité de protons agirait comme un petit déclencheur supplémentaire pour provoquer la fracture sur des failles déjà chargées de manière critique, produisant ainsi la corrélation observée pour les tremblements de terre à grande échelle.Une si petite perturbation s'ajouterait au principal facteur produisant la sismicité mondiale, qui est le stress tectonique.

Les références

1. 1.

   Corral, A. Diminution du temps et augmentation du temps jusqu'au prochain tremblement de terre. Phys. Rév. E 71 , 017101 (2005).

2. 2.

   Vecchio, A. et al. Propriétés statistiques du regroupement des séismes. Processus non linéaire. Géophys. 15 , 333 (2008).

3. 3.

   Corral, A. Lois d'échelle locales universelles par rapport aux lois d'échelle mondiales unifiées dans les statistiques de la sismicité. Phys. A 340 , 590 (2004).

4. 4.

   Carbone, V., Sorriso-Valvo, L., Harabaglia, P. & Guerra, I. Loi d'échelle unifiée pour les temps d'attente entre les événements sismiques. Europhys. Lett. 71 , 1036 (2005).

5. 5.

   Hasumi, T., Akimoto, T. & Aizawa, Y. La distribution Weibull–log Weibull pour les temps d'interoccurrence des séismes. Phys. A 388 , 491 (2009).

6. 6.

   Hasumi, T., Chen, C., Akimoto, T. & Aizawa, Y. La transition Weibull-log Weibull du temps d'interoccurrence pour les séismes synthétiques et naturels. Tectonophysique 485 , 9 (2010).

7. 7.

   Michas, G., Vallianatos, F. & Sammonds, P. Non-extensivité et corrélations à longue distance dans l'activité sismique au rift de West Corinth (Grèce). Processus non linéaire. Géophys. 20 , 713 (2013).

8. 8.

   Tsuruoka, H., Ohtake, M. & Sato, H. Test statistique du déclenchement des tremblements de terre par les marées : contribution de l'effet de charge des marées océaniques. Géophys. J. Int. 122 , 183 (1995).

9. 9.

   Vergos, G., Arabelos, DN & Contadakis, ME Preuve du déclenchement des marées sur les tremblements de terre de l'arc hellénique en Grèce. Phys. Chem. Terre 85-86 , 210 (2015).

10. dix.

    Bendick, R. & Bilham, R. Les faibles contraintes globales synchronisent-elles les tremblements de terre ?. Géophys. Rés. Lett. 44 , 8320 (2017).

11. 11.

    Shestopalov, IP & Kharin, EP Relation entre l'activité solaire et la sismicité globale et les neutrons d'origine terrestre. Russ. J. Terre Sci. 14 , ES1002. https://doi.org/10.2205/2014ES000536 (2014).

12. 12.

    Florindo, F. & Alfonsi, L. Forts séismes et secousses géomagnétiques : une relation de cause à effet ?. Anne. Géofis. 38 , 457-461 (1995).

13. 13.

    Florindo, F., Alfonsi, L., Piersanti, A., Spada, G. & Marzocchi, W. Secousses géomagnétiques et activité sismique. Anne. Géofis. 39 , 1227-1233 (1996).

14. 14.

    Florindo, F., De Michelis, P., Piersanti, A. & Boschi, E. Le tremblement de terre de Mw=9.3 Sumatra pourrait-il déclencher une secousse géomagnétique ?. EOS 86 (12), 123–124 (2005).

15. 15.

    Duma, G. & Ruzhin, Y. Changements diurnes de l'activité sismique et variations Sq géomagnétiques. Nat. Dangers Terre Syst. Sci. 3 , 171-177 (2003).

16. 16.

    Odintsov, S., Boyarchuk, K., Georgieva, K., Kirov, B. & Atanasov, D. Tendances à longue période de l'activité sismique et géomagnétique mondiale et leur relation avec l'activité solaire. Phys. Chem. Terre 31 , 88-93 (2006).

17. 17.

    Wolf, R. Sur le retour périodique du minimum de taches solaires : l'accord entre ces périodes et les variations de la déclinaison magnétique. PhiBartlos. Mag. 5 , 67 (1853).

18. 18.

    Simpson, JF L'activité solaire comme mécanisme de déclenchement des tremblements de terre. Planète Terre. Sci. Lett. 3 , 417-425 (1967).

19. 19.

    Huzaimy, JM & Yumoto, K. Corrélation possible entre l'activité solaire et la sismicité globale. En Proc. 2011 Conférence internationale IEEE sur les sciences spatiales et la communication. Penang Malaisie , 138-141 (2011).

20. 20.

    Rabeh, T., Miranda, M. & Hvozdara, M. Forts séismes associés à des variations géomagnétiques quotidiennes de grande amplitude. Nat. Dangers 53 , 561-574. https://doi.org/10.1007/s11069-009-9449-1 (2010).

21. 21.

    Sobolev, GA, Zakrzhevskaya, NA & Kharin, EP Sur la relation entre la sismicité et les orages magnétiques. Izvestiya Phys. Terre solide 37 , 917-927 (2001).

22. 22.

    Bakhmutov, VG, Sedova, FI & Mozgovaya, TA Perturbations géomagnétiques et tremblements de terre dans la zone de Vrancea. Izvestiya Phys. Terre solide 43 , 931-937 (2007).

23. 23.

    Gribbin, J. Relation entre les taches solaires et l'activité sismique. Science 173 , 558 (1971).

24. 24.

    Han, Y., Guo, Z., Wu, J. & Ma, L. Déclenchement possible de l'activité solaire à de grands tremblements de terre (Ms ≥ 8) dans des failles de direction ouest-est en Chine. Sci. Chine Ser. B Phys. Méca. Astron. 47 , 173-181. https://doi.org/10.1360/03yw0103 (2004).

25. 25.

    Sobolev, GA & Demin, VM Phénomènes électromécaniques de la Terre (Nauka, Moscou, 1980).

26. 26.

    Love, JJ & Thomas, JN Déclenchement solaire-terrestre insignifiant de tremblements de terre. Géophys. Rés. Lett. 40 , 1165-1170. https://doi.org/10.1002/grl.50211 (2013).

27. 27.

    Cafagna, A. La coopération CSES-Limadou. Dans 13th International Symposium on Radiation Physics, 7-11 septembre 2015, Pékin, Chine . https://doi.org/10.13140/RG.2.2.29807.84648 (2015).

28. 28.

    Storchak, DA et al. Publication publique du catalogue global instrumental des séismes ISC-GEM (1900-2009). Séisme. Rés. Lett. 84 , 810 (2013).

29. 29.

    Dziewonski, AM, Chou, TA & Woodhouse, JH Détermination des paramètres de source de tremblement de terre à partir de données de forme d'onde pour des études de sismicité mondiale et régionale. J. Géophys. Rés. 86 , 2825 (1981).

30. 30.

    Ekström, G., Nettles, M. & Dziewonski, AM Le projet mondial CMT 2004-2010 : Tenseurs de moment centroïde pour 13 017 tremblements de terre. Phys. Planète Terre. Inter. 200-201 , 1 (2012).

31. 31.

    Gutenberg, B. & Richter, CF Fréquence des tremblements de terre en Californie. Taureau. Sismol. Soc. Un m. 34 , 185 (1944).

32. 32.

    Bak, P., Christensen, K., Danon, L. & Scanlon, T. Loi d'échelle unifiée pour les tremblements de terre. Phys. Rév. Lett. 88 , 178501 (2002).

33. 33.

    Harabaglia, P. Probabilité d'occurrence de séismes non-poissoniens à travers des fonctions de survie empiriques. Appl. Sci. 10 , 838 (2020).

34. 34.

    Molchan, GM Stratégies dans la prévision des tremblements de terre forts. Phys. Planète Terre. Int. 61 , 84-98 (1990).

35. 35.

    Molchan, G. Structure des stratégies optimales dans la prévision des tremblements de terre. Tectonophysics 193 , 267-276 (1991).

36. 36.

    Jaeger, JC & Cook, NGV Fundamentals of Rock Mechanics 3e éd. (Chapman et Hall, Londres, 1979).

37. 37.

    Stein, RS, King, GCP & Lin, J. Modification de la contrainte de rupture sur le système de failles sud de San Andreas causée par le séisme de magnitude 1992 = 7:4 des Landers. Science 258 , 1328-1332 (1992).

38. 38.

    Troise, C., De Natale, G., Pingue, F. & Petrazzuoli, SM Preuve de l'interaction des contraintes statiques entre les tremblements de terre dans les Apennins centre-sud (Italie). Géophys. J. Int. 134 (3), 809-817. https://doi.org/10.1046/j.1365-246x.1998.00610.x (1998).

39. 39.

    Jánský, J. & Pasko, VP Lumières sismiques : mécanisme de couplage électrique de la croûte terrestre à la basse atmosphère. J. Géophys. Rés. Atmosphère. 123 , 8901-8914. https://doi.org/10.1029/2018JD028489 (2018).

40. 40.

    Hayakawa, M. et al. Une étude statistique sur la corrélation entre les perturbations ionosphériques inférieures vues par la propagation subionosphérique VLF/LF et les séismes. J. Géophys. Rés. 115 , A09305. https://doi.org/10.1029/2009JA015143 (2010).

41. 41.

    Hayakawa, M. Phénomènes électromagnétiques associés aux tremblements de terre. IEEJ Trans. Fundam. Mater. https://doi.org/10.1541/ieejfms.126.211 (2001).

42. 42.

    Losseva, TV & Nemchinov, IV Earthquake Lights et processus de rupture, dans « Evaluation des risques sismiques, phénomènes précurseurs et électromagnétisme sismique », Contadakis, M. et Biagi, PF eds.. Nat. Dangers Terre Syst. Sci. 5 , 649-656 (2005).

43. 43.

    Molchanov, O. et al. Couplage lithosphère-atmosphère-ionosphère en tant que mécanisme régissant les événements présismiques à court terme dans l'atmosphère et l'ionosphère. Nat. Dangers Terre Syst. Sci. 4 , 757-767. https://doi.org/10.5194/nhess-4-757-2004 (2004).

Télécharger les références

Remerciements

Données gracieusement fournies par l'expérience CELIAS/PM sur le vaisseau spatial Solar Heliospheric Observatory (SOHO). SOHO est une mission conjointe de l'Agence spatiale européenne et de la National Aeronautics and Space Administration des États-Unis. Trois relecteurs anonymes sont reconnus pour leur contribution à l'amélioration significative de l'article. Ce travail a été partiellement soutenu par le projet PON ARS01-00405 OT4CLIMA.

Informations sur l'auteur

Affiliations

1. Scuola di Ingegneria, Università della Basilicata, Via dell'Ateneo Lucano 10, 85100, Potenza, Italie

   Vito Marchitelli & Paolo Harabaglia

2. Département de la mobilité, des travaux publics, de l'écologie, de l'environnement, du gouvernement de la région des Pouilles, 70100, Bari, Italie

   Vito Marchitelli

3. Istituto Nazionale di Geofisica e Vulcanologia, Via Diocleziano 328, 80124, Naples, Italie

   Claudia Troise & Giuseppe De Natale

4. CNR-INO, Via Campi Flegrei 34, 80078, Pouzzoles, Italie

   Claudia Troise & Giuseppe De Natale

Contributions

PH a élaboré des programmes et des analyses statistiques; VM a travaillé l'idée originale; GDN et CT ont écrit l'essentiel de l'article ; tous les auteurs ont participé à l'analyse et à l'interprétation des données et ont contribué à la rédaction de la version finale.

auteur correspondant

Correspondance à Giuseppe De Natale .

Déclarations éthiques

Intérêts concurrents

Les auteurs ne déclarent aucun intérêt concurrent.

Source