Nous avons vu que ce modèle fut construit sur une période d’environ trente années et que des observations astronomiques récentes ont mises à mal les principales hypothèses effectuées dans le cadre de ce dernier.
Pour « sauver » le modèle, de nouvelles propositions ad-hoc et très spéculatives ont du être effectuées en inventant des concepts d’une vacuité flagrante tels que la matière et l’énergie dites « noires ». A l’issue de presque vingt années de recherches ayant mobilisé d’énormes moyens d’investigations (LHC, ISS, etc), aucune trace de ces dernières ne fut découverte.
La cosmologie est donc en crise depuis la fin du siècle dernier et les physiciens mainstream spécialistes de la question sont incapables de proposer un modèle solide en mesure de correspondre aux observations.
Il existe cependant un modèle alternatif développé par un physicien peu médiatisé qui résout les questions en suspens en étendant les concepts de la Relativité Générale ainsi que ceux du Modèle standard des particules [2].
Le physicien Jean-Pierre Petit propose donc le modèle « JANUS » développé en collaboration avec un certain nombre d’autres scientifiques sur une période d’environ quarante années (*).
(*) Gilles d’Agostini, Jean-Marie Souriau, William Bonnor, Frédéric Decamp, etc.
1. Les limitations majeures du modèle ΛCDM
A l’heure actuelle, il n’existe pas une seule grande théorie capable de modéliser l’ensemble des phénomènes allant de « l’infiniment petit » jusqu’à « l’infiniment grand ».
En effet, la Physique quantique modélise tous les phénomènes connus de l’Univers matériel à l’exception de la gravitation. Ce que l’on appelle « gravitation » concerne l’effet d’attraction apparent des masses de matières entres elles (exemple : attraction terrestre).
La gravitation fait donc l’objet d’une seconde grande théorie spécifique : la Relativité Générale.
Le modèle standard de la cosmologie [1] appelé également ΛCDM fait donc appel aux deux grandes théories élaborées au 20e siècle :
- Théorie Quantique
- Relativité Générale
Ces sauvetages successifs ont cependant été effectués au détriment de la crédibilité du modèle.
En effet, plusieurs concepts « exotiques » furent inventés tels que l’inflation ou alors un nom fut posé sur un mystère en considérant que « nommer, c’est résoudre » avec les fameuses matière et énergie dites noires.
Pour cette dernière, on ressortit de la naphtaline la constante cosmologique d’Einstein afin de rendre compatible l’équation de champs de la Relativité avec les observations.
(L’article précédent ici [1] détaille tous ces aspects).
Huit problèmes majeurs non (ou mal) résolus par ΛCDM
Les questions majeures non résolues par le modèle ΛCDM sont au nombre de huit :
1) Instant zéro
2) Dissymétrie entre matière et antimatière
3) Homogénéité du rayonnement fossile
4) Structure de l’Univers matériel en « éponge » avec de grands vides en forme de bulles
5) Stabilité des galaxies en rotation
6) Accélération de l’expansion cosmique
7) Mystères du « Great reppeller » et des sondes Pioneer
8) Courbures locales de l’espace anormalement importantes
Une nouvelle forme de matière à théoriser
Tous ces mystères nous indiquent qu’il existe des composants élémentaires de l’Univers que nous ne connaissons pas encore.
Nous ne ferons donc pas l’économie d’ajouter au bestiaire des particules du modèle standard (*) de la physique [2] un certain nombre d’éléments afin d’étendre ce dernier pour expliquer les observations.
Les matières et énergies « noires » évoquées par la cosmologie mainstream ne sont en aucune façon décrites par leurs caractéristiques. De plus, toutes les recherches expérimentales effectuées depuis plus de quinze ans pour découvrir la matière noire ont échoué.
(*) A ne pas confondre avec celui de la cosmologie.
L’hypothèse à laquelle s’accrochent obstinément les physiciens est que cette matière mystérieuse se comporte gravitationnellement de la même manière que celle que nous connaissons. Nous allons voir que si l’on fait sauter cette croyance bloquante, alors les choses changent radicalement !
On sait depuis le 17e siècle avec la théorie de la gravitation de Newton que les corps massifs s’attirent entre eux.
Einstein a généralisé cette théorie avec la Relativité Générale sans pour autant remettre en cause la validité des travaux de Newton.
Le modèle standard de la physique [2] décrit alors les quatre forces fondamentales incluant la gravitation, qui régissent le comportement des particules dans l’Univers.
L’histoire de l’Univers à grande échelle a été théorisée à partir de la force gravitationnelle qui aurait « sculpté » les grandes structures que l’on observe. Les trois autres forces n’interviennent que dans la vie des étoiles ou des atomes.
Le postulat de base fut de considérer une interaction gravitationnelle purement attractive, force est de constater que cette hypothèse ne suffit plus pour expliquer les observations.
Alors que faire ?
L’Univers à grande échelle [3] est constitué de matière baryonique (ordinaire) sous forme d’amas galactiques regroupés en filaments et alvéoles séparés par de grandes bulles en apparence vides d’environ 200 millions d’années lumière (AL) de diamètre.
Commençons alors par une analogie fromagère !
Première question : d’où viennent les trous de l’Emmental ?
L’Emmental, un fromage en expansion !
Les trous dans le fromage proviennent de minuscules particules de foin ayant infiltré le lait lors de la traite des vaches. Ces dernières servent alors d’amorces lors de la fermentation en dégageant du gaz carbonique qui vient ainsi creuser le fromage en créant des trous à l’intérieur de celui-ci.
En effet, le gaz carbonique se retrouve sous pression car, ne pouvant s’échapper, il est confiné à l’intérieur du fromage. Il provoque alors un effet répulsif centrifuge qui vient créer les fameuses bulles en apparence vides à l’intérieur de la meule et qui plus est provoquent une sorte d’expansion de cette dernière avec un bombage de la meule car la croute est imperméable.
Plus généralement, si l’on considère un bloc de matière malléable, comment arriver à faire apparaitre des bulles en son cœur ?
La seule possibilité consiste à mettre en œuvre des sources ponctuelles de pression à l’intérieur de ce bloc de manière à « repousser » la matière environnante, la pression qui s’exerce dans toutes les directions formera alors un volume sphérique dit de moindre énergie.
On observe un phénomène similaire lorsqu’un plongeur évacue de l’air sous l’eau, la pression de ce dernier crée des bulles sphéroïdales.
Bulles de vide dans Univers, un effet répulsif
Pour expliquer la formation des bulles de vide observées dans l’Univers, il faudrait donc envisager une forme de matière/énergie invisible mais gravitationnellement répulsive et concentrée au centre des ces dernières.
D’après la Relativité Générale, pour obtenir un effet répulsif, la seule possibilité est basée sur l’inversion du signe de la masse de la matière, autrement dit considérer une masse négative.
Cette idée fut explorée en 1957 par le physicien Hermann Bondi, elle fut cependant abandonnée pendant plus d’un demi-siècle car elle conduisait à des incohérences.
Hermann Bondi
Hermann Bondi partit donc de l’hypothèse de l’existence de masses matérielles négatives dans notre Univers.
Il appliqua alors l’équation d’Einstein à cette matière et il obtint un résultat mathématiquement cohérent.
Les calculs montrèrent les interactions suivantes entre les différents types de matière :
1) Les masses positives attirent toutes les autres masses
2) Les masses négatives repoussent toutes les autres masses
On voit immédiatement la contradiction, en effet, les masses positives et négatives s’attirent et se repoussent en même temps.
Si l’on poursuit cependant le calcul, on constate qu’un système constitué d’une masse positive et d’une masse négative va voir sa vitesse croitre à l’infini sans aucun apport d’énergie extérieure.
Ce phénomène fut appelé « effet runaway ».
Effet runaway
Même si le calcul est mathématiquement correct, le concept est physiquement absurde, en effet les mathématiques sont au service de la physique et pas l’inverse.
Suite à ces résultats, ce concept de masse négative ne fut plus étudié durant 57 ans jusqu’à la publication en 2014 de l’article de JP Petit et G D’Agostini [JPP 2014.1] dans la revue Astrophysics ans Space Science.
C’est ici qu’intervient le modèle Janus.
3. Introduction au modèle Janus
Avant d’aborder le modèle Janus, il convient de citer les travaux précurseurs du prix Nobel russe Andreï Sakharov.
Le physicien Russe Andreï Sakharov (1921-1989)
Dès les années 1960, Andreï Sakharov a proposé un modèle d’Univers double dit « jumeaux », le premier est bien entendu le notre et le second est inversé en partant à rebrousse temps (rétrochrone) à partir de la fameuse singularité ou « Instant « zéro » :
Univers double de Sakharov
Dans ce modèle, les deux Univers sont disjoints et symétriques (on dit en mathématiques « énantiomorphes ») et le temps s’écoule à l’envers dans le second.
Cependant, Sakharov n’a pas envisagé que ces deux Univers pourraient n’en former qu’un seul à cause de ce problème de temps inversé, ce point fut alors résolu par le mathématicien français Jean Marie Souriau [4].
Jean-Marie Souriau (1922-2012)
La géométrie symplectique est une branche peu connue de cette discipline développée par les mathématiciens Bertram Kostant et Alexandre Kirillov.
Souriau s’est alors appuyé sur les travaux de ces derniers afin de les appliquer à la physique en développant en 1970 la théorie des systèmes dynamiques [5].
Dans le cadre de cette théorie, Souriau a démontré que l’inversion du temps est équivalent à l’inversion du signe de l’énergie (Extrait en PDF de son livre ici).
(Voir la vidéo de JPP JANUS 13).
A partir de ce résultat, il fut aisé de confondre l’Univers jumeau de Sakharov avec le notre, il a suffit de retourner ce dernier un peu comme une chaussette :
Les deux Univers n’en font alors plus qu’un avec un premier sous-ensemble constitué de particules à énergie positive et un second sous-ensemble avec des particules à énergie négative, ces deux sous-ensembles interagissent entre eux à travers la gravitation jusqu’à aujourd’hui.
Restait alors à résoudre le problème de l’effet runaway incompatible avec la Relativité Générale.
L’introduction de masses négatives « indépendantes »
Pour s’affranchir de ce problème, le modèle Janus postule l’existence d’une matière de masse négative mais qui n’interagit pas avec la matière ordinaire que nous connaissons.
Pour ce faire, il faut d’une part enrichir le Modèle standard de la physique avec un nouveau jeu de particules et d’autre part étendre la Relativité Générale à ces dernières en considérant qu’elles « vivent leur vie » strictement entres elles.
Nous verrons par la suite qu’à l’instar des particules ordinaires de masse (+), les particules de masse (-) se regroupent en nuages pour former de grands conglomérats.
Le lien entre les masses positives et les masses négatives se fera par l’intermédiaire de l’espace-temps (*) qui sera courbé dans un sens par les premières et dans l’autre sens par les secondes.
(*) Commun à toutes les particules
Les quatre principes directeurs du modèle Janus
Le modèle Janus va alors modifier quatre secteurs fondamentaux de la physique :
– Enrichissement du modèle standard des particules
– Extension de la Relativité Générale
– Instant zéro et « constantes variables »
– Modélisation de la dissymétrie matière/antimatière
Ce modèle va donc en particulier modifier sensiblement les deux théories majeures mises au point au siècle dernier.
4. Le modèle Janus
Ce chapitre va présenter la synthèse des modifications apportées par le modèle Janus aux théories actuelles en commençant par le modèle standard de la physique des particules.
A. Enrichissement du modèle standard des particules
Le Modèle standard de la physique « 1.0 »
Le Modèle Standard de la physique [2] a établit un jeu de 25 particules différentes (*) qui suffisent à décrire tous les phénomènes constatés par la physique expérimentale sauf la gravitation qui est théorisée par la Relativité Générale.
(*) Non comptées les particules d’antimatière de charge électrique inversée.
Les 25 particules à masse positive du modèle standard
Les particules du Modèle Standard forment deux grandes familles avec d’une part les fermions (Quarks et Leptons), en gros des particules dites matérielles possédant une masse et d’autre part les bosons, particules sans masse (sauf les Z et W) qui sont les vecteurs d’interactions entre les fermions.
Toutes ces particules possèdent plusieurs propriétés physiques dont nous retiendrons ici principalement :
– la masse
– l’énergie pour les particules de masse nulle
– la charge électrique
– des règles d’interaction
La notion de masse
La masse est une forme d’énergie concentrée, masse (m) et énergie (E) sont reliées par la célèbre formule d’Einstein E = mc2 (c = vitesse de la lumière).
Intuitivement, la masse représente une quantité de matière mais il ne s’agit pas d’un concept aussi simple qu’on pourrait le croire.
Elle est représentés selon deux formes en mécanique classique avec la masse gravitationnelle et la masse inertielle considérées comme égales en Relativité Générale.
La physique quantique utilise également une notion de masse pour les particules qui serait acquise grâce au fameux boson de Higgs.
Cependant, la masse quantique et la masse relativiste sont traitées indépendamment l’une de l’autre car ces deux théories sont incompatibles.
Dans ces deux théories, la masse est cependant considérée comme toujours positive pour ce qui concerne la matière détectable.
Énergie
L’énergie est un concept assez complexe à définir, elle existe sous plusieurs formes : électromagnétique, cinétique, de masse, etc.
Elle est également considérée aujourd’hui comme une grandeur toujours positive (+) qui se conserve lorsqu’elle change de nature à travers des transformations physiques.
Charge électrique et antimatière
La charge électrique est une propriété fondamentale des particules, elle est théorisée par l’électromagnétisme et la QED [6].
Par convention, la charge électrique des particules de matière fut choisie négative pour l’électron et donc positive pour le proton afin que l’atome soit électriquement neutre. Il existe également des particules à charge inversée qui constituent l’antimatière (ex : le positron est l’antiparticule de l’électron, il possède les mêmes caractéristiques sauf sa charge électrique qui est positive).
Chaque particule du modèle standard possède son antiparticule (*), en cas de rencontre elles se retransforment en photons.
(*) Certaines particules sont leur propre antiparticule (ex : photon).
Règles d’interactions entre les particules
Les fermions possèdent des règles d’interactions parfaitement définies suivant les 4 forces fondamentales qui se manifestent par des bosons associés :
– interaction forte (Bosons = gluons)
– interaction faible (Bosons = W+, W-, Z0)
– interaction électromagnétique (Boson = photon)
– interaction gravitationnelle (Boson hypothétique = graviton)
Lorsqu’une particule interagit suivant une ou plusieurs de ces 4 forces, cette interaction se produit par échanges de bosons associés. La seule interaction qui concerne 100% des particules -y compris les bosons- est la gravitation, cependant l’existence du graviton est loin d’être démontrée. La gravitation est pour l’instant uniquement décrite par la Relativité Générale.
Les particules du modèle standard à masse positive (m+) et leurs interactions possibles
Les quarks sont les constituants des hadrons (protons/neutrons), ils sont sensibles à toutes les interactions.
Le neutrino n’est sensible qu’à l’interaction faible et à la gravitation, c’est la raison pour laquelle il est difficile à détecter.
L’électron quand à lui est sensible à toutes les forces sauf l’interaction forte.
Le modèle Janus ajoute alors un nouveau jeu de particules selon des principes similaires au modèle standard.
La particularité de ces deux ensembles de particules est que, hormis pour la gravitation, elles interagissent uniquement entre particules de la même famille. Par exemple, les photons d’énergie négative γ(-) n’interagissent pas avec les électrons d’énergie positive e(+), ces photons « négatifs » sont donc indétectables par nos appareils de mesures… œil humain inclus !
Janus, vers un Modèle standard de la physique « 2.0 »
Les particules ajoutées par le modèle Janus sont donc presque des jumelles des particules du modèle standard ci-dessus avec des différence de masses/énergies et de charges électriques.
25 nouvelles particules à masse négative
On ajoute donc 25 nouvelles particules dont les particularités sont les suivantes :
1) Masses ou énergies négatives : m(-) ou E(-)
2) Valeurs absolues des masses m(-) et énergies E(-) beaucoup plus élevées que celles des particules ordinaires m(+) et E(+).
3) Trois des quatre interactions de la physiques n’ont lieu qu’entre des particules de même signe de masse/énergie, les particules m(-) n’interagissent qu’avec les particules m(-), idem pour les particules m(+).
4) Les particules des deux espèces m(+), γ(+) et m(-), γ(-) interagissent toutes ensembles à travers la gravitation.
Cette partie reste à développer.
Remarquons à ce niveau que les deux espèces de particules n’en forment probablement qu’une seule et qu’elles ne font que changer de référentiel lors du changement de signe de leur masse/énergie avec un mécanisme dont le détail reste à préciser.
Interactions possibles entre les particules des deux espèces
Coté interaction gravitationnelle, c’est le domaine de la Relativité Générale qu’il va cette fois falloir modifier
B. Relativité Générale : Janus ajoute une seconde équation de champ
Rappelons brièvement que la Relativité Générale est basés sur les trois points suivants :
1) L’espace (3D) et le temps (t) sont reliés entres eux sous la notion d’espace-temps (3D+t)
2) La matière-énergie courbe géométriquement l’espace-temps
3) L’espace-temps impose les trajectoires de déplacement (*) à la matière et à l’énergie
(*) Nommées « géodésiques ».
Lors de la genèse de la Relativité Générale, Einstein a travaillé avec le grand mathématicien David Hilbert, ce dernier l’aurait grandement aidé pour la formulation de son équation de champs. N’oublions pas également la contribution déterminante à la RG des brillants travaux de Riemann sur les géométries courbes effectués un demi-siècle auparavant.
Nous présentons ci-dessous la première forme de l’équation de champs d’Einstein telle que ce dernier l’a publiée le 25 novembre 1915.
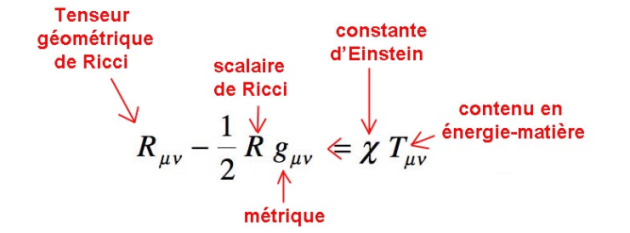
1) Le terme de droite définit le contenu de l’espace-temps en énergie-matière (Tμν = tenseur énergie-impulsion)
2) Celui de gauche indique sa géométrie
3) Le terme gμν est l’inconnue de cette équation, il s’agit de ce que l’on appelle une métrique. Une métrique permet de calculer des trajectoires (*) dans l’espace-temps.
(*) Un exemple concret : la résolution de cette équation restreinte au cas du système solaire permettrait de calculer la trajectoire (métrique) d’une sonde naviguant entre les planètes, ces dernières courbant localement l’espace-temps.
Dans le cas de la Relativité Générale, le terme de droite fut choisit avec de la matière de masse strictement positive m(+).
-> La question de la constante cosmologique
En 1915, la croyance partagée par les physiciens était basée sur un Univers stationnaire, en effet l’expansion n’avait pas encore été détectée.
Pour « forcer » son équation à se plier à la vision de l’époque, Albert Einstein y ajouta donc un ingrédient mathématique ad-hoc appelé « constante cosmologique« . On voit dans cet exemple que la physique n’est autre qu’une « cuisine » que l’on modifie lorsque la saveur souhaitée n’est pas au rendez-vous des équations !
En 1917, la seconde forme de l’équation de champs fut publiée :
Au début des années 1920, coup de théâtre, l’astronome Vesto Slipher découvre le fameux décalage vers le rouge des nébuleuses lointaines. Cette découverte fut rapidement interprétée comme la signature d’un Univers en expansion par l’abbé Lemaître (article paru en 1927) avant que la paternité de cette découverte n’en revienne injustement à Edwin Hubble en 1929.
Et donc en 1923, Einstein écrit au mathématicien Weyl :
« Si l’Univers n’est pas statique, alors au diable la constante cosmologique ! ».
D’après le russe Georges Gamov, Einstein fit même une déclaration apocryphe sur le fait que l’introduction de cette constante fut la plus grande erreur de sa carrière.
On ne parla plus de cette fameuse constate cosmologique durant presque un siècle lorsqu’elle fut ressortie du placard avec le modèle ΛCDM [1] dans les années 2000.
Dans ce modèle, la constante cosmologique permet de prendre en compte l’accélération de l’expansion découverte en 1998 par Perlmutter, Schmidt et Riess (prix Nobel 2011).
-> Le modèle JANUS remplace l’équation de champs de la Relativité Générale par deux équations
Le physicien Jean-Pierre Petit est donc parti de l’équation de champs d’Einstein pour la transformer en un système de deux équations à deux inconnues.
Les équations de champs de Petit sont les suivantes :
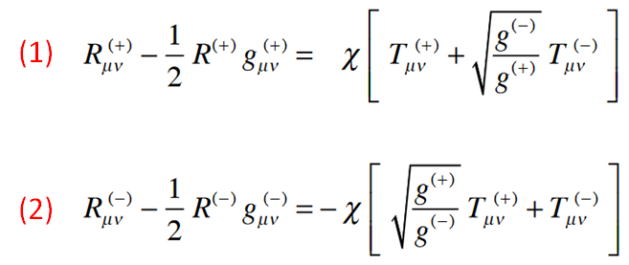
Elles se présentent sous la forme d’un système de deux équations dont les deux inconnues sont les métriques g(+)μν et g(-)μν. La métrique g(+)μν s’applique aux particules d’énergie positives et la métrique g(-)μν à celles d’énergie négative (*).
On distingue dans le membre de droite de chaque équation le tenseur énergie-impulsion « Tμν« , il s’agit de la contribution de l’énergie totale de l’Univers constituée de celle qui est positive T(+)μν et de celle qui est négative T(-)μν..
(*) On simplifie la terminologie en ne parlant ici que de particules d’énergie. En effet, cette dernière se présente soit sous forme de rayonnements sans masses (photons), soit sous forme de particules matérielles de masse m avec la relation E=mc2.
Cette formulation traduit bien le fait que les masses positives ET les masses négatives courbent toutes les deux l’espace-temps.
Tout corps solide ou gazeux ne peut être constitué que de matière dont la masse possède le même signe (+) ou (-) car, comme vu précédemment, seules les particules dont l’énergie est de même signe peuvent s’assembler entres elles.
Il existe dons deux cas de figure selon que nous percevions les masses positives (c’est notre cas) ou les masses négatives :
1) Étant dans un état de type « masses positives », nous détectons dans le cosmos un excès de courbure (g(+)μν) induit par les masse négatives nous étant invisibles.
2) Si l’on arrivait à inverser notre masse de manière à passer en « masses négatives », alors on détecterait « symétriquement » la contribution des masses positives à la courbure inverse (g(-)μν) que l’on percevrait. A la place des vides détectés entre les amas de galaxies lumineuses, nous percevrions de gigantesques sphéroïdes rougeoyants constitués de matière négative attractive pour la matière m(-) et répulsive pour la matière m(+).
Cas où la matière de masse positive est prépondérante
On remarque que dans une zone de l’espace où la densité de matière négative est négligeable devant celle de matière positive, alors le terme T(-)μν sera proche de zéro.
On retrouve alors la formulation de l’équation de champs initiale d’Einstein « vue depuis les masses positives » sans constante cosmologique :
Les constantes g et c sont différentes pour les deux familles de particules
Les constantes telles que vitesse de la lumière ou gravitation sont de valeurs différentes entre les deux types d’environnements, en effet, pour les particules d’énergie négative, ces dernières sont beaucoup plus élevées.
(Voir la vidéo de JPP JANUS 15).
-> Le modèle JANUS fait disparaitre le paradoxe de l’effet Runaway
Le calcul de Bondi qui menait au paradoxe Runaway consistait à appliquer aux masses positives et aux masses négatives une équation unique, soit l’équation de champs d’Einstein.
Cette fois, nous appliquons une équation différente aux masses positives et aux masses négatives, et alors le calcul montre que le paradoxe Runaway disparait.
Pour retrouver la notion de forces, on effectue ce que l’on nomme une approximation Newtonienne qui consiste à considérer de faibles courbures de l’espace-temps (cas du système solaire par exemple), alors on trouve les relations suivantes :
Les masses positives s’attirent selon la loi de Newton
Les masses négatives s’attirent selon la loi de Newton
Les masses de signes opposés se repoussent selon « anti-Newton »
On obtient donc cette fois un modèle physiquement cohérent :
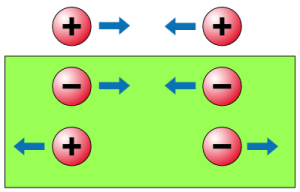
Modèle Janus
© Travaux publiés en 2014 [JPP2014-1].
-> Compatibilité ascendante des théories gravitationnelles de Newton, Einstein et Petit
En synthèse, nous obtenons un nouveau modèle plus général qui assure une compatibilité ascendante avec les modèles précédents :
Compatibilité ascendante des trois modèles de la gravitation
C. Instant zéro et constantes variables
C. Instant zéro et constantes variables
Le problème de l’instant « zéro » a été abordé dans les articles suivants : ici et ici.
Le modèle standard de la cosmologie évoque un temps infinitésimal dit « temps de Planck », en deçà duquel la théorie quantique ne s’applique plus car nous sommes en dessous du « plus petit élément possible de temps ».
Cependant, la notion de temps n’a plus de sens dans une soupe primordiale où toutes les particules sont proches de la vitesse de la lumière, en effet à cette vitesse, le temps ne s’écoule plus !
On pourra alors calculer le nombre de tours de cette horloge au voisinage de l’instant zéro.
-> Un modèle à constantes variables
Nous avons vu dans l’article précédent [1] que les calculs de la progression de l’horizon cosmologique durant l’expansion montraient que cet horizon n’avait pas permis d’échanges d’informations entre toutes les particules du fond cosmologique. En conséquence, sa remarquable homogénéité en température était inexplicable.
C’est pourquoi le concept controversé « d’inflation » fut proposé.
Il existe une autre explication, en effet, si l’on suppose que la vitesse de la lumière fut plus élevée durant la phase radiative, alors les particules auraient pu interagir pour homogénéiser leur température.
Cependant, dans cette hypothèse, les équations de la physique (thermodynamique, quantiques, ….) ne fonctionnent plus….sauf si l’on suppose que toutes les « constantes » varient en même temps pour :
1) Conserver la validité des équations (*).
2) Assurer la conservation de l’énergie.
(*) Équations de Schrödinger, de champs d’Einstein, de Boltzmann et de Maxwell.
Variation des constantes durant l’ère radiative
Avec ce modèle, la taille de l’horizon cosmologique « suit » l’expansion de l’Univers jusqu’à la date de 380 000 ans, date où laquelle les constantes se stabilisent.
Le problème de l’homogénéité du fond cosmologique fossile disparait alors sans faire appel à l’inflation.
(Voir la vidéo de JPP JANUS 23).
-> Instant zéro
Avec ce modèle, si l’on calcule le nombre de tours de notre horloge élémentaire en se rapprochant de l’origine, on trouve que ce dernier tend vers l’infini !
L’Univers n’aurait donc pas de début…
D. Dissymétrie matière/antimatière
Ce mystère n’est pas à proprement une nouveauté apportée par le modèle Janus, cette partie reprend en fait les travaux du prix Nobel Andreï Sakharov.
Sakharov est en effet le premier a avoir proposé un premier niveau d’explication au mystère de l’absence d’antimatière de masse positive.
D’après ce dernier, la nucléosynthèse des quarks et antiquarks aurait produit en quantité égale ces deux espèces.
S’est alors ensuivie la Baryogénèse ou formation des protons et neutrons (baryons) ainsi que de leurs antiparticules (antibaryons) formés par l’assemblage de trois quarks.
A travers les trois conditions dites de Sakharov, ce dernier émet alors l’hypothèse que l’assemblage des baryons serait un peu plus rapide que celui des antibaryons, et donc lorsque la température de l’Univers descendit en dessous du seuil de création de ces derniers [1], il serait resté un excédent de baryons (dont l’utilité ne fait aucun doute !) ainsi qu’un résidu d’antiquarks « libres » ne s’étant jamais assemblés entre eux, ce dernier résidu serait alors toujours présent.
Des antiquarks encore présents à l’état libre ?
Ce problème est loin d’être résolu, cependant des expériences telles que « BaBar » semblent avoir mis en évidence l’une des conditions de Sakharov, soit la violation de symétrie CP (PDF).
Les recherches sont en cours sur cette question qui pourrait avoir un impact majeur sur le modèle standard de la physique.
(Voir la vidéo de JPP JANUS 12)
5. Modifications apportées par Janus sur l’histoire de l’Univers
Le déroulé de l’histoire de l’Univers décrit dans le modèle standard [1] reste valable dans ses grandes lignes.
Cependant, la « soupe cosmique » initiale présente maintenant deux populations de particules distinctes qui n’interagissent pas entres elles (*) :
– les particules d’énergie positive
– les particules d’énergie négatives
(*) Un peu comme si l’on secouait un mélange d’eau et d’huile dans un flacon.
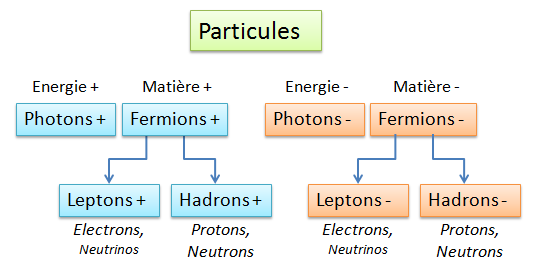
L’énergie individuelle des particules négatives est cependant très supérieure à celle d’énergie positives. Cette caractéristique se retrouvera alors sur les masses des particules de types « fermions négatifs » créées par collisions de photons à hautes énergies négatives.
Le différentiel des masses m(-) est pour l’instant estimée entre 8 et 64 fois la masse m(+) des particules « ordinaires ». Cette valeur reste à mesurer précisément à l’aide d’observations indirectes des masses de matière négatives.
Avant la transition de l’Univers vers la phase matière, la gravitation était négligeable devant les trois autres interactions possibles entre les particules. Comme vu plus haut, les particules d’énergie négatives eurent une histoire très voisine de celles des particules positives.
Les deux familles de particules évoluent indépendamment
→ Environ 34 minutes après le big bang
A l’issue de la phase radiative nous avons donc la situation suivante :
⇒ famille énergie positive
. Fermions m(+) : noyaux d’hydrogène prépondérants, noyaux d’hélium, électrons
⇒ famille énergie négative
. Fermions m(-) (*) : noyaux d’hydrogène prépondérants (*), noyaux d’hélium, électrons
(*) Il s’agit en fait d’anti-fermions de charges électriques inversées, mais nous oublierons pour l’instant cet aspect afin de ne pas complexifier l’explication.
→ Transition vers la phase matière : 380 000 ans après le big bang
Dans cette phase, nous avons donc un double découplage photons/électrons avec :. la libération des électrons de masse (+) permettant la constitution des atomes m(+) d’hydrogène et d’hélium
. la libération des électrons de masse (-) permettant la constitution des atomes m(-) d’hydrogène et d’hélium
Avec une densité des particules de masses négatives très supérieure à celle des particules de masse positive.
Situation à la sortie de la phase radiative
A la sortie de la phase radiative, la situation de l’Univers est la suivante :
- Famille de particules de masse positive : 87% d’hydrogène m(+) et 13% d’Hélium m(+)
- Famille de particules de masse négative : hydrogène m(-) et Hélium m(-), les ratios sont à déterminer
- Un fond cosmologique de photons à énergie positive E(+)
- Un fond cosmologique de photons à énergie négative E(-), indétectable pour nous.
Les bases du modèle Janus étant posées, voyons maintenant comment ce dernier explique les huit principales questions non résolues par le modèle ΛCDM.
6. Janus répond aux questions sans réponses de ΛCDM
Question 1 : instant zéro
D’après ΛCDM, le premier intervalle de temps de l’Univers (temps de Planck) est hors des lois de la physique connue, nous sommes donc dans une singularité, terme employé pour nommer un inconnu total.
Avec le modèle Janus à constantes variables, cette barrière disparait car le temps de Planck (quanta) diminue au fur et à mesure de l’approche du « point zéro ».
Comme vu précédemment avec notre horloge conceptuelle, une image didactique de l’Univers ressemblerait à un livre d’épaisseur finie où la page en cours est le présent, les pages suivantes le futur.
Lorsque l’on tourne les pages vers le passé, ces dernières sont de plus en plus minces et leur nombre tend vers l’infini lorsque l’on se rapproche de la page 1 !
Question 2 : dissymétrie entre matière et antimatière
Comme on l’a vu précédemment, pour une famille de particules, la vitesse de fabrication des particules de matière à partir des quarks serait différente de celle des particules d’antimatière.
Coté masses positives, le résultat est donc un léger surplus de matière (*) avec un fond résiduel d’antiquarks correspondant.
Coté masses négatives, à l’inverse on obtient un léger surplus d’antimatière avec un fond résiduel de quarks de masses négatives correspondant.
On remarque une symétrie entre la famille résiduelle de particules à masses positives constituée de matière et la famille résiduelle à masses négatives constituée d’antimatière. Les nombres baryoniques et leptoniques de l’Univers entier seraient ils nuls ?
(*) constituant tout de même tout l’Univers visible !
(**) Ne pas confondre la masse et la charge électrique.
Question 3 : homogénéité du rayonnement fossile
Grace au modèle à constantes variables dans le début de la vie de l’Univers, l’horizon cosmologique a suivi l’expansion permettant une communication à vitesse luminique entre les particules expliquant la température homogène du rayonnement fossile.
On remarque que la vitesse de la lumière tend vers l’infini lorsque l’on se rapproche de l’instant zéro.
(Voir les vidéos de JPP JANUS 18 et JANUS 19).
Question 4 : structure de l’Univers matériel en éponge avec de grands vides sphéroïdaux
La fabrication des grandes structures
→ Horloge cosmique : de 380 000 ans à 0.5 Milliards d’années
Après le double découplage, l’instabilité gravitationnelle théorisée par James Jeans commence à jouer son rôle, les premiers effondrements de nuages d’hydrogènes ont lieu d’abord pour la matière négative du fait de sa plus importante densité.
Les premières grandes structures constituées de proto-étoiles (*) d’hydrogène de masse négative m(-) vraisemblablement regroupées en amas forment des sphéroïdes plus ou moins réguliers constituant la charpente de l’Univers.
Ces structures tendent alors à repousser la matière positive qui prend une forme alvéolaire (effet « emmental ») favorable au refroidissement ultérieur du cœur des proto-étoiles.
Ce n’est que dans un second temps que les nuages d’hydrogène « positifs » vont s’effondrer à leur tour pour constituer cette fois des étoiles qui vont « s’allumer ».
(*) Les proto-étoiles de masse négatives seront à jamais incapables de démarrer des réactions de fusion pour constituer de véritables étoiles à cause de leur masse gigantesque.
Simulations informatiques
Des simulations 2D effectuées en 1992 sur le système informatique du centre DESY de Hambourg ont été effectuées par un jeune chercheur en contact avec Jean-Pierre Petit.
En appliquant l’approximation Newtonienne sur 5000 points-masses de matière négative et 5000 points-masses de matière positive avec un facteur de densité relative de 64, les simulations ont donné un résultat conforme aux observations astronomiques.
C’est le seul modèle capable de représenter la genèse de l’Univers observable.
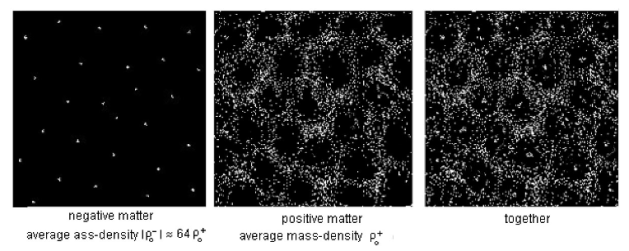Simulations de 1992 sur 10 000 points masses de matières (+) et (-) On distingue sur la vue de gauche les agglomérats de matière négative se constituant en premiers, ces derniers repoussent la matière positive créant ainsi une géométrie alvéolaire (image centrale).
La vue de droite montre l’ensemble des deux familles de matière.
Ces simulations demanderaient à être poursuivies en travaillant cette fois en 3D et avec prise en compte de l’expansion cosmique (*). Les capacités de traitement des machines actuelles permettent de travailler sur un nombre de points masses de plusieurs milliards qui permettraient d’obtenir une grande précision dans les résultats.
©Travaux publiés publiés en 1995 dans la revue « Astrophysics and Space Science » [JPP1995].
(*) La question des conditions aux limites serait aisément résolue en travaillant sur une hypersphère S3.
Question 5 : stabilité des galaxies en rotation
-> Janus explique la stabilité des galaxies spirales en rotation
Contrairement à ce que l’on pourrait croire, la rotation des galaxies spirales sur elles mêmes pose un énorme problème. En effet, un calcul simple d’attraction gravitationnelle montre que les étoiles périphérique devraient être éjectées de leur orbite sous l’effet de la force centrifuge induite par leur rotation (*).
(*) L’année galactique du soleil (un tour complet) vaut environ 250 millions d’années.
Le modèle Janus répond à ce problème jamais résolu en considérant que les galaxies sont confinées par un environnement extérieur de matière de masse négative.
Les simulations 2D effectuées également en 1992 montrent la genèse d’une galaxie à partir d’un nuage de gaz condensé qui se met en rotation puis se stabilise et perdure durant des dizaines de tours, soit une durée supérieure à l’age de l’Univers.
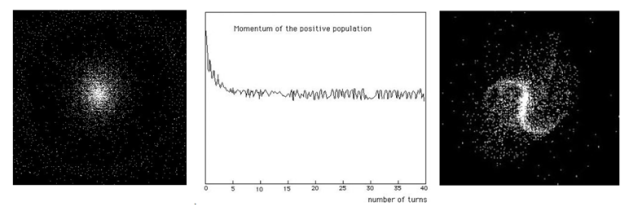Simulation d’une galaxie spirale (droite) à partir d’un nuage de gaz (gauche) Résultat à comparer avec l’exemple de la galaxie NGC 1300 observée par le télescope Hubble :
Galaxie NGC 1300
Le principe sous-jacent à ce modèle de galaxies en rotation est celui de la tasse de café avec un nuage de lait (confiné par la tasse) !
-> Janus explique l’accélération de l’expansion de l’Univers
A la sortie de l’ère dite radiative, soit à 380 000 ans après le début, nous nous trouvons en présence de deux Univers de poussière qui évoluent conjointement.
Une solution exacte des deux équations de champs de Petit démontre que l’accélération de l’expansion est due à l’influence des masses négatives.
L’expansion sera cependant vue différemment selon que l’on considère la métrique associée aux masses positives ou celle des masses négatives.
© Travaux publiés en 2014 [JPP2014-1].
Point de vue des masses positives
L’expansion « vue depuis les masses positives » obéit à une équation découverte par le mathématicien Wiliam Bonnor.
La courbe obtenue avec cette équation montre une accélération de l’expansion se confondant parfaitement avec les observations :
Observations et courbe Janus
Point de vue des masses négatives
Point de vue des masses négatives
L’expansion « vue depuis les masses négatives » quand lui décélère et obéit à un modèle classique de Friedman.
Le fait que l’on détermine une décélération est certes contre intuitif, mais reste parfaitement cohérent à partir du moment où l’on a deux métriques différentes qui déterminent deux manières différentes de mesurer les distances.
Coté masses positives, on a une vitesse de la lumière et une certaine mesure des distances et coté masses négatives, une vitesse de la lumière plus élevée et des distances apparentes….plus courtes !
(Voilà du grain à moudre pour les philosophes).
(Voir la vidéo de JPP JANUS 16).
© Travaux publiés en 2014 [JPP2014-2].
Question 7 : mystère du « Great Repeller » et des sondes Pioneer
Le Great Repeller découvert en 2016 (PDF) est tout simplement constitué d’un conglomérat de masses négatives (cluster) qui repousse les masses positives dans son voisinage selon « anti-Newton ».
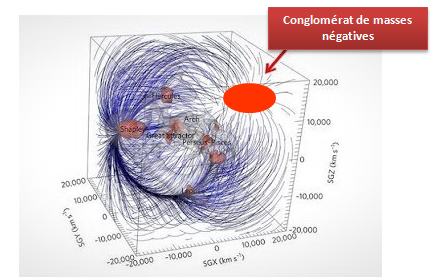
Le mystère du « Great repeller » résolu
Et pour le cas du ralentissement des sondes Pioneer, ces dernières sont entrées dans une zone où il existe une relativement faible densité de matière négative suffisante cependant pour induire un ralentissement de ces dernières.
(Voir la vidéo de JPP JANUS 17).
Question 8 : courbures locales de l’espace anormalement importantes
Considérons une galaxie A placée derrière un amas B qui, d’après la Relativité Générale courbe l’espace dans son voisinage. L’observateur X va donc constater un effet de lentille gravitationnel supposé lié uniquement à l’influence de l’amas B.
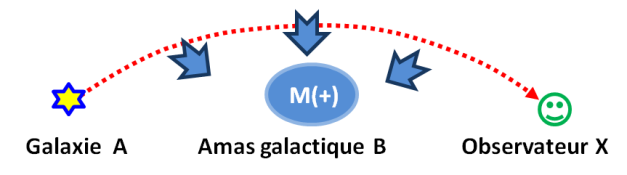Cependant, les calculs à partir de l’équation d’Einstein montrent que la quantité de matière détectée dans l’amas B ne suffit pas à expliquer la courbure constatée en C. Le modèle ΛCDM fait l’hypothèse d’une matière noire supplémentaire B’ située au même endroit que B afin que la masse totale (B +B’) corresponde à la courbure constatée.
⇒ C’est cette matière noire qui est recherchée depuis plus de 20 ans sans succès…
Le modèle Janus postule quand à lui que notre amas B est entouré d’un halo de matière négative C qui va « repousser » l’espace au voisinage de B, il s’agit d’un effet gravitationnel inverse de celui que provoque la matière ordinaire.
La contribution à la courbure de l’amas B seul sera faible par rapport à celui de la matière du halo D.
Tout ceci est vérifié cette fois par le calcul de la métrique des masses positives g(+)μν.
A ce niveau, remarquons que pour un observateur fait de masses négatives, la lumière (énergie négative) émise par un conglomérat négatif D serait déviée dans l’autre sens par le halo C et dans une moindre mesure par l’amas B (calculable avec la métrique g(-)μν).
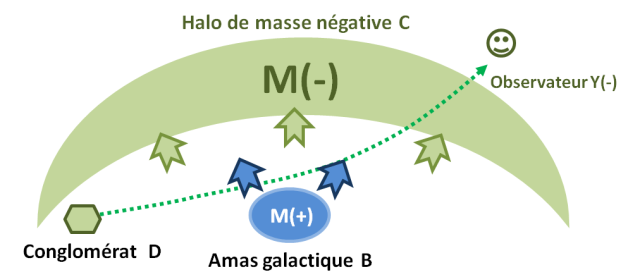
(Voir la vidéo de JPP JANUS 20).
7. Conclusion
Le modèle Janus est royalement ignoré par la majorité de la communauté cosmologique devenue de nos jours une sorte de coterie particulièrement sclérosée.
Fait aggravant, il n’existe aucune autre théorie aussi aboutie qui répond à la plupart des questions non résolues par ΛCDM.
Ce n’est pas la première fois (et à coup sur pas la dernière) qu’un scientifique aura eu raison contre l’ensemble de la communauté, l’épistémologie regorge d’exemples allant dans ce sens.
Citons le cas de Galilée qui défendit le modèle héliocentrique de Copernic contre d’une part les tenants des théories aristotéliciennes et d’autre part le puissant pouvoir religieux de l’époque (la laïcité était encore loin).
Autre cas, celui de Ludwig Boltzman fervent partisan de l’atomisme ayant eu raison avant tout le monde et qui finit par se suicider devant l’hostilité de ses pairs.
Le fait de proposer une théorie à contre courant ne suffit pas bien entendu pour en déduire qu’elle est meilleure que celle qu’elle remplace. Cependant, à partir du moment où une théorie est conceptuellement explicite et mathématiquement robuste, et surtout capable de proposer des explications là où sa concurrente ne dit rien, alors elle mérite à minima d’être prise au sérieux et examinée de près.
L’histoire des sciences nous a également montré que même si une bonne théorie ne s’impose pas toujours d’elle même, ce sont ses détracteurs qui finissent par disparaitre, ce n’est peut être qu’une question de temps pour que la Relativité Générale soit remplacée par le modèle Janus et l’équation de champs d’Einstein par les équations de Petit !
Article source :
https://zevengeur.wordpress.com/2018/01/12/histoire-de-lunivers-partie-6-modele-janus-le-futur-de-la-cosmologie/
Liens :
[1] Histoire de l’univers – Partie 5 : Grandeur et décadence du modèle standard de la cosmologie
[2] Histoire de l’univers – Partie 4 : Le Modèle standard de la physique
[3] Mille Milliards de soleils (Sur ce site)
[4] Site officiel de Jean-Marie Souriau ici.
[5] Structure des systèmes dynamiques – JM Souriau (1970)
[6] Histoire de l’univers – Partie 3 : QED…vous avez dit QED ? (Sur ce site)
[7] Site Jean-Pierre PETIT ici.
Documents publiés par Jean-Pierre PETIT en relation avec le modèle Janus :
Chaine Youtube JPP (23 vidéos Janus) ici.
https://www.youtube.com/user/JPPETITofficiel
Site JPP : modèle cosmologique Janus ici.
http://www.jp-petit.org/science/JANUS_COSMOLOGICAL_MODEL/JMC.htm
Bande dessinée JPP : « L’Univers gémellaire » – PDF ici.
« Modèle Janus – 40 années de travail » – PDF ici.
« L’Univers Janus – Partie 1 » – PDF ici.
« L’Univers Janus – Partie 2 » – PDF ici.
Livres :
« On a perdu la moitié de l’Univers » – JP Petit (Albin Michel 1997)
« OVNI L’extraordinaire découverte – JP Petit & JC Bourret (Trédaniel 2017)
Articles JPP dans revues à comité de lectures :
[JPP1995] J.P.Petit : « Twin Universe Cosmology »
Astrophysics and Space Science (1995) – p. 226, 273‐307.
[JPP 2014.1] J.P.Petit and G.D’Agostini : « Negative mass hypothesis and the nature of dark energy« .
Astrophysics and Space Science (2014) 354 : 611-615 20 sept 2014 DOI 10.1007/s10509-014-2106-5
[JPP 2014.2] J.P.Petit and G.D’Agostini : « Cosmological bimetric model with interacting positive and negative masses and two different speeds of light in agreement with the observed acceleration of_the Universe ».
Modern Physics Letters A. – Vol. 29, No. 34 (24 oct. 2014) 1450182 (15 pages) DOI : 10.1142/S021773231450182X
[JPP 2015.1] J.P.Petit and G.D’Agostini : « Cancellation of the singularity of the Schwarzschild solution with natural mass inversion process« .
Modern Physics Letters A – vol. 30 n°9 2015
[JPP 2015.2] J.P.Petit and G.D’Agostini : « Lagrangian derivation of the two coupled fields equations in the Janus cosmological model ».
Astrophysics and Space Science – (2015) 18 apr 2015, 357:67
Aucun commentaire:
Enregistrer un commentaire
Remarque : Seul un membre de ce blog est autorisé à enregistrer un commentaire.